【培优版】浙教版（2024）七上第六章 图形的初步认识 单元测试
试卷日期：2025-02-12 考试类型：单元试卷
一、选择题（本题有10小题，每小题3分，共30分）
-
1. 如图，下列说法中，错误的是（ ）
A、点B在直线上 B、点A在直线外 C、点C在线段上 D、点M在线段的延长线上2. 下列说法错误的是（ ）A、直线与直线是同一条直线 B、线段与线段是同一条线段 C、射线与射线是同一条射线 D、射线与线段都是直线的一部分3. 观察图形，下列说法正确的有（ ）（ 1 ）直线和直线是同一条直线；（2）线段和线段是两条不同的线段；（3）射线和射线是同一条射线；（4）三条直线两两相交时，一定有三个交点．
A、1个 B、2个 C、3个 D、4个4. 物理中的打印技术通过读取截面相关的信息，用液体状、粉状或片状的材料将这些截面逐层打印出来，再将各层面以多种方式粘合起来，从而制造出一个实体．莲花中学数学兴趣小组利用打印机，读取到截面的相关信息有三角形、梯形和六边形，那么打印机可能打出来的是哪一种立体图形（ ）A、圆柱 B、圆锥 C、四棱锥 D、正方体5. 如图，AB是一段高铁行驶路线图，图中字母表示的5个点表示5个车站.在这段路线上往返行车，需要印制车票 （ ）
A、10种 B、11种 C、20种 D、22种6. 将∠A 与∠B 两个角的关系记为∠A =n∠B(n>0)，探索n 的大小与两个角的类型之间的关系。下列说法正确的是( )A、当n=2时，若∠A 为锐角，则∠B 为锐角 B、当n=2时，若∠A 为钝角，则∠B 为钝角 C、当 时，若∠A 为锐角，则∠B 为锐角 D、当 时，若∠A 为锐角，则∠B 为钝角7. 如图所示的4×4的方格中，记∠ABD=α，∠DEF=β，∠CGH=γ，则( )
A、β<γ<α B、β<α<γ C、α<γ<β D、α<β<γ8. 如果线段AB=13cm，MA+MB=17 cm，那么下面说法中正确的是（ ）.A、M点在线段AB上 B、M点在直线AB上 C、M点在直线AB外 D、M点可能在直线AB上，也可能在直线AB外9. 如图，在公路上有A、M、C、B、N、D任意六点，点为直线外一点，连接、、、、、 ， 下列结论：①在直线l上的线段共有15条；②若平分 ， 平分 ， ， 则；③若M为的中点，N为的中点，则；④若 ， ， 则 ． 正确的有（ ）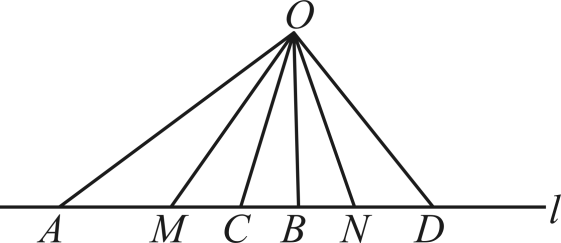
A、1个 B、2个 C、3个 D、4个二、填空题（本题有6小题，每小题4分，共24分）
-
10. 一条直线上取A ， B ， C ， D四个点时，共得条线段，条射线；
11. 如图，A，B，C，D，E，P，Q，R，S，T是构成五角星的五条线段的交点，则图中共有条线段.
12. 如图，已知AB=12，延长BA至点C，使 ， D 为线段 BC 的中点，则 AD 的长为.
13. 如图，线段 ， ， ， E是的中点，在线段上取点D，使得 ， 则的长度为 ．
14. 如图，点C，D在线段BE上（C在D的左侧），点A在线段BE外，连接AB，AC，AD，AE，已知∠BAE ＝ 120°，∠CAD ＝ 60°，有下列说法：①直线CD上以B，C，D，E为端点的线段共有6条；②作∠BAM＝ ∠BAD，∠EAN＝ ∠EAC.则∠MAN＝30°；③以A为顶点的所有小于平角的角的度数和为420°；④若BC＝2，CD＝DE＝3，点F是线段BE上任意一点，则点F到点B，C，D，E的距离之和最大值为17，最小值为11.其中说法正确的有 .（填上所有正确说法的序号）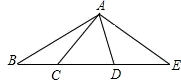
15. 如图1， 为直线 上一点，作射线 ，使 ，将一个直角三角尺如图摆放，直角顶点在点 处，一条直角边 在射线 上.将图1中的三角尺绕点 以每秒10°的速度按逆时针方向旋转（如图2所示），在旋转一周的过程中，第 秒时， 所在直线恰好平分 ，则 的值为.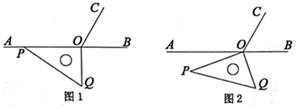
三、解答题（本题共8小题，第17题6分，第18题10分，第19题6分，第20题6分，第21题8分，第22题10分，第23题10分，第24题10分，共66分）
-
16. 如下图，用圆规和直尺作线段AB ， 使（不写作法，保留作图痕迹）．
17. 如图，已知四点A、B、C、D，请用尺规作图完成．（保留画图痕迹）
(1)、画直线；(2)、画射线；(3)、连接并延长到E，使得；(4)、在线段上取点P，使的值最小，你的依据是 ．18. 已知一个立方体的体积为100cm3 ， 求它的表面积(精确到1cm2)．19. 如图，C为线段上一点，点B为的中点，且 ， ，
(1)、求的长；(2)、若点E在直线上，且 ， 求的长.20. 如图所示，点O在直线AE 上，∠AOB=40°，∠EOD=28°46' ， OD 平分∠COE，求∠COB 的度数.
21. 问题提出：某校要举办足球赛，若有5 支球队进行单循环比赛（即全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场），则该校一共要安排多少场比赛?【构建模型】生活中的许多实际问题，往往需要构建相应的数学模型，利用模型的思想来解决问题．为解决上述问题，我们构建如下数学模型：
(1)、如图①，我们可以在平面内画出5 个点（任意 3个点都不在同一条直线上），其中每个点各代表一支足球队， 两支球队之间比赛一场就用一条线段把他们连接起来．由于每支球队都要与其他各队比赛一场，即每个点与另外4个点都可连成一条线段，这样一共连成条线段，而每两个点之间的线段都重复计算了一次，实际只有条线段，所以该校共要安排场比赛；(2)、根据图②的规律，若学校有 n支足球队进行单循环比赛，则该校一共要安排场比赛；(3)、【类比迁移】从同一个顶点引出6条射线，共可以组成个角；(4)、【实际应用】往返于枣庄和济南的同一辆高速列车，途经滕州东站、曲阜东站、泰安3个车站（每种车票票面都印有上车站名称与下车站名称），那么在这段线路上往返行车，要准备的车票为多少种?22. 如图1，点C在线段上，图中有三条线段，分别为线段和 ， 若其中一条线段的长度是另外一条线段长度的2倍，则称点C是线段的“智慧点”．
(1)、线段的中点______这条线段的“智慧点”（填“是”或“不是”）；(2)、若线段 ， 点C为线段的“智慧点”，则______；(3)、如图2，已知， ， 动点P从点A出发，以的速度沿AB向点B运动，点Q从点B出发，以的速度沿向点A运动，点P、Q同时出发，当其中一点到达终点时，运动停止，设运动的时间为t秒，若A、P、Q三点中，一点恰好是以另外两点为线段的“智慧点”，求出所有可能的t值．23.
(1)、特例感知：如图 ， 线段 ， ， 线段在线段上运动（点不超过点 ， 点不超过点），分别是的中点．在线段运动的过程中，线段的长度是否发生变化？如果不变，求出的长度；如果变化，请说明理由；(2)、知识迁移：我们发现角的很多规律和线段一样，如图 ， 在内部转动，射线和射线分别平分和 ． ①若 ， ， 则 ▲ ；
②请你猜想 ， 和三个角具有怎样的数量关系，并说明理由；(3)、类比探究：如图 ， 在内部转动，若 ， ， ， ， 直接写出用含有的式子表示的度数．