【基础版】浙教版（2024）七上第六章 图形的初步认识 单元测试

试卷日期：2025-02-12 考试类型：单元试卷

前去【出卷网】下载

一、选择题（本题有10小题，每小题3分，共30分）

  • 1. 下列三个生活，生产现象：
    ①用两个钉子就可以把木条固定在墙上；

    ②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线；
    ③把弯曲的公路改直，就能缩短路程．
    其中可用基本事实＂两点确定一条直线＂来解释的现象有

    A、①③
     B、①②
     C、②③
     D、③

    查看试题解析

  • 2. 在朱自清的《春》中描写春雨“像牛毛、像花针、像细丝，密密麻麻地斜织着”的语句，这里把雨看成了线，这说明了（    ）
    A、点动成线 B、线动成面 C、面动成体 D、两点确定一条直线

    查看试题解析

  • 3. 下列各图中，表示“射线AB”的是 ( )
    A、 B、 C、 D、

    查看试题解析

  • 4. 如图，有下列结论：①以点A为端点的射线共有5条；②以点D为端点的线段共有4条；③射线CD和射线DC是同一条射线；④直线BC和直线EF是同一条直线。其中正确的是  (   )

    A、①② B、①④ C、②③ D、②④

    查看试题解析

  • 5. 如图，∠AOB=90° ， OD是∠AOC的平分线．若∠BOC=32° ， 则∠AOD的度数为（     ）

    A、15° B、29° C、32° D、58°

    查看试题解析

  • 6. 如图标注的图形名称与图形不相符的是（　　）
    A、 B、 C、 D、

    查看试题解析

  • 7. 如图，是直角顶点重合的一副三角板，若∠BCD=40° ， 下列结论错误的是（     ）

    A、∠ACD=130° B、∠ACD=∠BCE C、∠ACE=130° D、∠ACE−∠BCD=100°

    查看试题解析

  • 8. 若∠1+∠2=180° ， ∠2+∠3=180° ， 则∠1与∠3的关系是（  ）
    A、互补 B、互余 C、相等 D、无法确定

    查看试题解析

  • 9. 如图，点B，C，D在线段AE上，已知BD=3,BD=13AE,则图中所有线段的长度之和为 (   )

    A、42 B、48 C、50 D、56

    查看试题解析

  • 10. 有公共端点P的两条线段MP，NP组成一条折线M-P-N，若该折线 M-P-N上一点Q把这条折线分成相等的两部分，我们把这个点Q叫作这条折线的“折中点”。已知点D是折线A-C-B的“折中点”，E为线段AC的中点，CD=6，CE=10，则线段BC的长是(   )
    A、8 B、8或16 C、8或32 D、16或32

    查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

  • 11. 已知一个角的补角是它的余角的3倍，则这个角的度数为。

    查看试题解析

  • 12. 已知A，B，C都是直线l上的点，且AB＝5 cm，BC＝3 cm，那么点A与点C之间的距离是 ．

    查看试题解析

  • 13. 如图，AB=12cm ， 若C为AB的中点，点D在线段AC上，且CD:CB=2:3 ， 则DB的长度为 ．

    查看试题解析

  • 14. ∠1与∠2互余，∠2与∠3互补，∠1=63° ， 那么∠3= ．

    查看试题解析

  • 15. 体育课上，小悦在点 O处进行了四次铅球试投，铅球分别落在图中的M，N，P，Q 四个点处，则表示她最好成绩的是点。

    查看试题解析

  • 16. 如图，射线OA，OB 把∠POQ 三等分，若图中所有小于平角的角的度数之和是300°，则∠POQ 的度数为。

    查看试题解析

三、解答题（本题共8小题，第17题6分，第18题6分，第19题10分，第20题8分，第21题8分，第22题8分，第23题10分，第24题10分，共66分）

  • 17. 如图，根据要求使用尺规完成下列作图（不写作法，保留作图痕迹）：

    (1)、作线段AC ， 射线AB ， 直线AD；
    (2)、请在直线AD上画出一点N ， 使得BN+CN的和最小．

    查看试题解析

  • 18. 如图，直线AB、CD相交于点O，OM⊥AB．

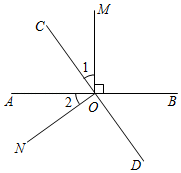    (1)、若∠1＝∠2，证明：ON⊥CD；
    (2)、若∠1=13∠BOC，求∠BOD的度数．

    查看试题解析

  • 19. 如图，C为线段AD上一点，点B为CD的中点，且AD=9cm ， BD=2cm ．

    (1)、图中共有条线段；
    (2)、求AC=______；
    (3)、若点E在直线AD上，且EA=3cm ， 求BE的长．

    查看试题解析

  • 20.  直线AB， CD 相交于点O.
    (1)、OE， OF 分别是 ∠AOC,∠BOD的平分线. 画出这个图形.
    (2)、射线OE， OF 在同一条直线上吗? 为什么?

    查看试题解析

  • 21. 如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分，我们称该点为这条折线的“折中点”．已知点D是图中折线A−C−B的“折中点”，请解答以下问题：

    (1)、①若AC=6,BC=10 ， 点D在线段（填“AC”或“BC”）上；②若AC=8,CD=3 ， 则BC的长度为 ．
    (2)、若E为线段AC的中点，EC=8,CD=6 ， 求CB的长度．

    查看试题解析

  • 22. 如图，已知∠AOB=120° ， OC是∠AOB内的一条射线，且∠AOC:∠BOC=1:2 ．

    (1)、求∠AOC的度数；
    (2)、过点O作射线OD ， 若∠AOD=12∠AOB ， 求∠COD的度数．

    查看试题解析

  • 23. 线段和角有很多相似之处，如都可以度量，都能进行大小比较等.小滨根据“角可以看成是一条射线绕着它的端点旋转而成的图形”研究了一个问题：

    (1)、【操作发现】如图，射线OT从OA 出发，绕着端点O以每秒2°的速度逆时针旋转，回到OA位置时，停止旋转.当射线OT 旋转24秒时到达OB位置，继续旋转30秒，到达OC位置，若OD平分∠BOC，求∠AOD 的度数.
    (2)、【特例研究】在上述条件下，若射线OT 从OC 出发，继续旋转m秒，问是否存在m，使得OB⊥OT? 若存在，求m的值；若不存在，请说明理由.

    查看试题解析

  • 24. 小敏在元旦期间参加登山活动，她携带了一根登山杖。如图①，这款可伸缩登山杖共有三节，我们把登山杖的三节类似看成三条线段，其中上节EF是固定不动的，长为54 m，它比中节CD长7cm，中节CD又比下节AB长3cm。如图②，在无伸缩的初始状态下，点D，E重合，点B，C也是重合的。

    (1)、求无伸缩的初始状态下登山杖AF的总长度。
    (2)、如图③，登山过程中，需要根据不同地形调整登山杖的长度，当总长度AF 短为116cm，且C恰为AE 的中点时，求缩进部分BC，DE 长。

    查看试题解析