5.分式——北师大版数学2025年中考一轮复习测

试卷日期：2025-02-04 考试类型：一轮复习

前去【出卷网】下载

一、选择题（每题3分，共36分）

1. 式子 $\frac{x^{3} + y}{x}$ ， $\frac{1}{2} (m + n)$ ， $\frac{1}{a}$ ， $\frac{2 x}{π - 1}$ ， $\frac{m - n}{m + n}$ ， $\frac{15 - π R^{2}}{y}$ 中，分式有 $()$ 个

A、 $6$ B、 $5$ C、 $4$ D、 $3$

查看试题解析
2. 如果分式 $\frac{x}{x - 1}$ 有意义，那么x的取值范围是（）

A、 $x > 1$ B、 $x \neq 0$ C、 $x \neq 1$ D、 $x < 1$

查看试题解析
3. 如果一个分式的分子或分母可以因式分解，且不可约分，那么我们称这个分式为“和谐分式” $.$ 下列分式中，是“和谐分式”的是( )

A、 $\frac{x^{2} - y^{2}}{x - y}$ B、 $\frac{x + y}{x^{2} - x y + y^{2}}$ C、 $\frac{4 x + 2 y}{x^{2} - 4 y^{2}}$ D、 $\frac{x^{2} - 2 x y + y^{2}}{2 x - 2 y}$

查看试题解析
4. 若将分式 $\frac{3 x}{x + 5 y}$ 中的x ， y都扩大10倍，则分式的值（　　）

A、扩大为原来的10倍 B、缩小为原来的 $\frac{1}{10}$ C、缩小为原来的 $\frac{1}{100}$ D、不改变

查看试题解析
5. 如图，一个正确的运算过程被盖住了一部分，则被盖住的是（）

A、 $\frac{1}{x - 3}$ B、 $\frac{x + 3}{x - 3}$ C、2 D、1

查看试题解析
6. 分式 $\frac{2 x^{2} y}{{(x + y)}^{2}}$ 与 $\frac{x^{2}}{x^{2} - y^{2}}$ 的最简公分母是（）

A、 $x^{4} - y^{4}$ B、 ${(x + y)}^{2} (x^{2} - y^{2})$ C、 ${(x - y)}^{4}$ D、 ${(x + y)}^{2} (x - y)$

查看试题解析
7. 下面的计算过程中，从哪一步开始出现错误（）.

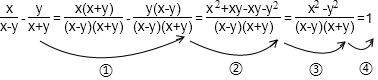A、① B、② C、③ D、④

查看试题解析

二、填空题（每题3分，共15分）

8. 要使分式 $\frac{3}{x - 3}$ 有意义，则 $x$ 应满足的条件是．

查看试题解析
9. 化简 $(\frac{x^{2}}{x - 3} + \frac{9}{3 - x}) \div \frac{x + 3}{2 x}$ 的结果是．

查看试题解析
10. 若式子 $\frac{\sqrt{x}}{x - 2}$ 有意义，则x的取值范围为．

查看试题解析

三、解答题（共7题，共49分）

11. 先化简，再求 $\frac{m^{2} - 4 m + 4}{m - 1} \div (\frac{3}{m - 1} - m - 1)$ 值，其中 $m = \sqrt{2} - 2$

查看试题解析
12. 先化简再求值： $(\frac{a - 1}{a} - \frac{a - 2}{a + 1}) \div \frac{2 a^{2} - a}{a^{2} + 2 a + 1}$ ；其中 $a^{2} - a - 1 = 0$ .

查看试题解析
13.

(1)、先化简，再求值： $(1 - \frac{1}{x + 2}) \div \frac{x^{2} - 1}{x + 2}$ .其中 $x = 3$ .

(2)、解分式方程： $\frac{x}{x - 2} - 1 = \frac{3}{x^{2} - 4}$

查看试题解析
14. 阅读材料：
材料1：法国数学家弗朗索瓦・韦达于1615年在著作《论方程的识别与订正》中建立了方程根与系数的关系，提出一元二次方程 $a x^{2} + b x + c = 0$ （ $a \neq 0$ ， $b^{2} - 4 a c \geq 0$ ）的两根 $x_{1}$ ， $x_{2}$ 有如下的关系（韦达定理）： $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} \cdot x_{2} = \frac{c}{a}$ ；
材料2：已知一元二次方程 $x^{2} - x - 1 = 0$ 的两个实数根分别为 $m$ ， $n$ ，求 $m^{2} n + m n^{2}$ 的值．
解： $∵$ 一元二次方程 $x^{2} - x - 1 = 0$ 的两个实数根分别为 $m$ ， $n$ ，
$∴ m + n = 1$ ， $m n = - 1$ ，则 $m^{2} n + m n^{2} = m n (m + n) = - 1 \times 1 = - 1$ ．
材料3：如果实数 $m$ 、 $n$ 满足 $m^{2} - m - 1 = 0$ 、 $n^{2} - n - 1 = 0$ ，且 $m \neq n$ ，则可利用根的定义构造一元二次方程 $x^{2} - x - 1 = 0$ ，然后将 $m$ 、 $n$ 看作是此方程的两个不相等实数根去解决相关问题．
根据上述材料，结合你所学的知识，完成下列问题：
（1）材料理解：
一元二次方程 $2 x^{2} - x - 1 = 0$ 的两个根为 $m$ ， $n$ ，则 $m + n =$ ______， $m n =$ ______， $\frac{1}{m} + \frac{1}{n} =$ ______．
（2）类比应用：已知实数 $s$ 、 $t$ 满足 $2 s^{2} - s - 1 = 0$ ， $2 t^{2} - t - 1 = 0$ ，且 $s \neq t$ ，求 $\frac{1}{s} - \frac{1}{t}$ 的值．
（3）思维拓展：已知 $x_{1}$ ， $x_{2}$ 是一元二次方程 $4 k x^{2} - 4 k x + k + 1 = 0$ 的两个实数根．直接写出使 $\frac{x_{1}}{x_{2}} + \frac{x_{2}}{x_{1}}$ 的值为整数的实数 $k$ 的整数值．

查看试题解析