广东省历年（2016-2024）中考数学真题压轴解答题汇编

试卷日期：2025-01-27 考试类型：二轮复习

前去【出卷网】下载

一、综合题

1. 如图，抛物线 $y = \frac{3 + \sqrt{3}}{6} x^{2} + b x + c$ 与 $x$ 轴交于 $A$ ， $B$ 两点，点 $A$ ， $B$ 分别位于原点的左、右两侧， $B O = 3 A O = 3$ ，过点 $B$ 的直线与 $y$ 轴正半轴和抛物线的交点分别为 $C$ ， $D$ ， $B C = \sqrt{3} C D$ ．

(1)、求 $b$ ， $c$ 的值；

(2)、求直线 $B D$ 的函数解析式；

(3)、点 $P$ 在抛物线的对称轴上且在 $x$ 轴下方，点 $Q$ 在射线 $B A$ 上，当 $Δ A B D$ 与 $Δ B P Q$ 相似时，请直接写出所有满足条件的点 $Q$ 的坐标．

查看试题解析
2. 平面直角坐标系 $x O y$ 中，抛物线 $G ： y = a x^{2} + b x + c (0 < a < 12)$ 过点 $A (1 ， c - 5 a)$ ， $B (x_{1} ， 3)$ ， $C (x_{2} ， 3)$ ，顶点 $D$ 不在第一象限，线段 $B C$ 上有一点 $E$ ，设 $△ O B E$ 的面积为 $S_{1}$ ， $△ O C E$ 的面积为 $S_{2}$ ， $S_{1} = S_{2} + \frac{3}{2}$ ．

(1)、用含 $a$ 的式子表示 $b$ ；

(2)、求点 $E$ 的坐标；

(3)、若直线 $D E$ 与抛物线 $G$ 的另一个交点 $F$ 的横坐标为 $\frac{6}{a} + 3$ ，求 $y = a x^{2} + b x + c$ 在 $1 < x < 6$ 时的取值范围（用含 $a$ 的式子表示）．

查看试题解析
3. 如图，点C为△ABD的外接圆上的一动点（点C不在 $\overset{⌢}{B A D}$ 上，且不与点B，D重合），∠ACB=∠ABD=45°

(1)、求证：BD是该外接圆的直径；

(2)、连结CD，求证： $\sqrt{2}$ AC=BC+CD；

(3)、若△ABC关于直线AB的对称图形为△ABM，连接DM，试探究DM² ， AM² ， BM²三者之间满足的等量关系，并证明你的结论．

查看试题解析
4. 如图，抛物线 $y = x^{2} + b x + c$ （b，c是常数）的顶点为C，与x轴交于A，B两点， $A (1 ， 0)$ ， $A B = 4$ ，点P为线段 $A B$ 上的动点，过P作 $P Q ∥ B C$ 交 $A C$ 于点Q．

(1)、求该抛物线的解析式；

(2)、求 $△ C P Q$ 面积的最大值，并求此时P点坐标．

查看试题解析
5.
如图，BD是正方形ABCD的对角线，BC=2，边BC在其所在的直线上平移，将通过平移得到的线段记为PQ，连接PA、QD，并过点Q作QO⊥BD，垂足为O，连接OA、OP．

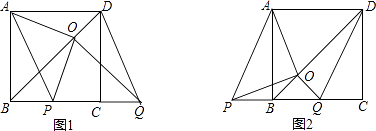(1)、请直接写出线段BC在平移过程中，四边形APQD是什么四边形？

(2)、请判断OA、OP之间的数量关系和位置关系，并加以证明；

(3)、在平移变换过程中，设y=S_△_OPB ， BP=x（0≤x≤2），求y与x之间的函数关系式，并求出y的最大值．

查看试题解析
6.
如图，在平面直角坐标系中，O为原点，四边形ABCO是矩形，点A，C的坐标分别是A（0，2）和C（2 $\sqrt{3}$ ，0），点D是对角线AC上一动点（不与A，C重合），连结BD，作DE⊥DB，交x轴于点E，以线段DE，DB为邻边作矩形BDEF．

(1)、填空：点B的坐标为；

(2)、是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD的长度；若不存在，请说明理由；

(3)、①求证： $\frac{D E}{D B}$ = $\frac{\sqrt{3}}{3}$ ；
②设AD=x，矩形BDEF的面积为y，求y关于x的函数关系式（可利用①的结论），并求出y的最小值．

查看试题解析
7. 如图，在菱形ABCD中，∠BAD = 120°，AB = 6，连接BD ．

(1)、求BD的长；

(2)、点E为线段BD上一动点（不与点B，D重合），点F在边AD上，且BE= $\sqrt{3}$ DF，
①当CE丄AB时，求四边形ABEF的面积；

②当四边形ABEF的面积取得最小值时，CE+ $\sqrt{3}$ CF的值是否也最小？如果是，求CE+ $\sqrt{3}$ CF的最小值；如果不是，请说明理由．

查看试题解析
8. 综合运用
如图1，在平面直角坐标系中，正方形 $O A B C$ 的顶点A在 $x$ 轴的正半轴上，如图2，将正方形 $O A B C$ 绕点 $O$ 逆时针旋转，旋转角为 $α (0 ° < α < 45 °)$ ， $A B$ 交直线 $y = x$ 于点 $E$ ， $B C$ 交 $y$ 轴于点 $F$ ．

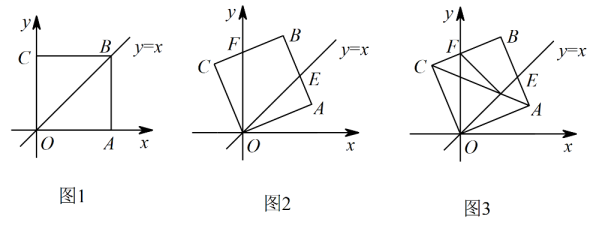(1)、当旋转角 $∠ C O F$ 为多少度时， $O E = O F$ ；（直接写出结果，不要求写解答过程）

(2)、若点 $A (4 ， 3)$ ，求 $F C$ 的长；

(3)、如图3，对角线 $A C$ 交 $y$ 轴于点 $M$ ，交直线 $y = x$ 于点 $N$ ，连接 $F N$ ，将 $△ O F N$ 与 $△ O C F$ 的面积分别记为 $S_{1}$ 与 $S_{2}$ ，设 $S = S_{1} - S_{2}$ ， $A N = n$ ，求 $S$ 关于 $n$ 的函数表达式．

查看试题解析
9. 已知二次函数 $y = a x^{2} + b x + c$ 的图象过点 $(- 1 ， 0)$ ，且对任意实数x ，都有 $4 x - 12 \leq a x^{2} + b x + c \leq 2 x^{2} - 8 x + 6$ ．

(1)、求该二次函数的解析式；

(2)、若（1）中二次函数图象与x轴的正半轴交点为A ，与y轴交点为C；点M是（1）中二次函数图象上的动点．问在x轴上是否存在点N ，使得以A、C、M、N为顶点的四边形是平行四边形．若存在，求出所有满足条件的点N的坐标；若不存在，请说明理由．

查看试题解析
10. 如图，在四边形ABCD中，∠B=60°，∠D=30°，AB=BC．

(1)、求∠A+∠C的度数。

(2)、连接BD，探究AD，BD，CD三者之间的数量关系，并说明理由。

(3)、若AB=1，点E在四边形ABCD内部运动，且满足 $A E^{2} = B E^{2} {+CE}^{2}$ ，求点E运动路径的长度。

查看试题解析
11. 如图，在菱形ABCD中， $∠ D A B = 60 °$ ， $A B = 2$ ，点E为边AB上一个动点，延长BA到点F ，使 $A F = A E$ ，且CF、DE相交于点G

(1)、当点E运动到AB中点时，证明：四边形DFEC是平行四边形；

(2)、当 $C G = 2$ 时，求AE的长；

(3)、当点E从点A开始向右运动到点B时，求点G运动路径的长度．

查看试题解析
12. 已知抛物线G： $y = m x^{2} - 2 m x - 3$ 有最低点。

(1)、求二次函数 $y = m x^{2} - 2 m x - 3$ 的最小值（用含m的式子表示）；

(2)、将抛物线G向右平移m个单位得到抛物线G₁_。经过探究发现，随着m的变化，抛物线G₁顶点的纵坐标y与横坐标x之间存在一个函数关系，求这个函数关系式，并写出自变量x的取值范围；

(3)、记（2）所求的函数为H，抛物线G与函数H的图像交于点P，结合图像，求点P的纵坐标的取值范围.

查看试题解析
13. 已知抛物线 $G : y = a x^{2} - 6 a x - a^{3} + 2 a^{2} + 1 (a > 0)$ 过点 $A (x_{1}, 2)$ 和点 $B (x_{2}, 2)$ ，直线 $l : y = m^{2} x + n$ 过点 $C (3, 1)$ ，交线段 $A B$ 于点 $D$ ，记 $△ C D A$ 的周长为 $C_{1}$ ， $△ C D B$ 的周长为 $C_{2}$ ，且 $C_{1} = C_{2} + 2$ ．

(1)、求抛物线 $G$ 的对称轴；

(2)、求 $m$ 的值；

(3)、直线 $l$ 绕点 $C$ 以每秒 $3 °$ 的速度顺时针旋转 $t$ 秒后 $(0 \leq t < 45)$ 得到直线 $l^{'}$ ，当 $l^{'} ∥ A B$ 时，直线 $l^{'}$ 交抛物线 $G$ 于 $E$ ， $F$ 两点．
①求 $t$ 的值；
②设 $△ A E F$ 的面积为 $S$ ，若对于任意的 $a > 0$ ，均有 $S \geq k$ 成立，求 $k$ 的最大值及此时抛物线 $G$ 的解析式．

查看试题解析
14. 如图1，在平面直角坐标系中，抛物线 $y = \frac{\sqrt{3}}{8} x^{2} + \frac{3 \sqrt{3}}{4} x - \frac{7 \sqrt{3}}{8}$ 与 $x$ 轴交于点 $A$ 、 $B$ （点 $A$ 在点 $B$ 右侧），点 $D$ 为抛物线的顶点.点 $C$ 在 $y$ 轴的正半轴上， $C D$ 交 $x$ 轴于点 $F$ ， $Δ C A D$ 绕点 $C$ 顺时针旋转得到 $Δ C F E$ ，点 $A$ 恰好旋转到点 $F$ ，连接 $B E$ .

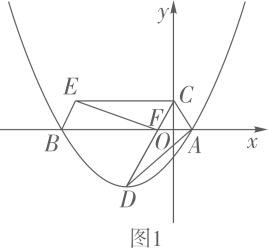
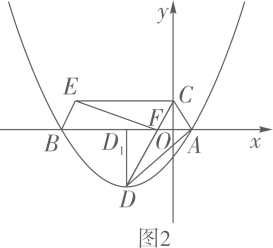(1)、求点 $A$ 、 $B$ 、 $D$ 的坐标；

(2)、求证：四边形 $B F C E$ 是平行四边形；

(3)、如图2，过顶点 $D$ 作 $D D_{1} ⊥ x$ 轴于点 $D_{1}$ ，点 $P$ 是抛物线上一动点，过点 $P$ 作 $P M ⊥ x$ 轴，点 $M$ 为垂足，使得 $Δ P A M$ 与 $Δ D D_{1} A$ 相似（不含全等）.
①求出一个满足以上条件的点 $P$ 的横坐标；

②直接回答这样的点 $P$ 共有几个？

查看试题解析
15. 如图，在正方形 $A B C D$ 中， $E$ 是边 $A D$ 上一动点 $($ 不与点 $A$ ， $D$ 重合 $) .$ 边 $B C$ 关于 $B E$ 对称的线段为 $B F$ ，连接 $A F$ ．

(1)、若 $∠ A B E = 15 °$ ，求证： $△ A B F$ 是等边三角形；

(2)、延长 $F A$ ，交射线 $B E$ 于点 $G$ ．
①△BGF能否为等腰三角形？如果能，求此时 $∠ A B E$ 的度数；如果不能，请说明理由；

$②$ 若 $A B = \sqrt{3} + \sqrt{6}$ ，求 $△ B G F$ 面积的最大值，并求此时 $A E$ 的长．

查看试题解析
16. 如图，AB是⊙O的直径， $\hat{A C}$ = $\ha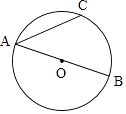t{B C}$ ，AB=2，连接AC．

(1)、求证：∠CAB=45°；

(2)、若直线l为⊙O的切线，C是切点，在直线l上取一点D，使BD=AB，BD所在的直线与AC所在的直线相交于点E，连接AD．
（Ⅰ）试探究AE与AD之间的是数量关系，并证明你的结论；
（Ⅱ）是否为定值？若是，请求出这个定值；若不是，请说明理由．

查看试题解析
17. 已知Rt△OAB，∠OAB=90°，∠ABO=30°，斜边OB=4，将Rt△OAB绕点O顺时针旋转60°，如题图1，连接BC．

(1)、填空：∠OBC=°；

(2)、如图1，连接AC，作OP⊥AC，垂足为P，求OP的长度；

(3)、如图2，点M，N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止，已知点M的运动速度为1.5单位/秒，点N的运动速度为1单位/秒，设运动时间为x秒，△OMN的面积为y，求当x为何值时y取得最大值？最大值为多少？

查看试题解析
18. 【问题背景】
如1图，在平面直角坐标系中，点B，D是直线 $y = a x (a > 0)$ 上第一象限内的两个动点 $(O D > O B)$ ，以线段BD为对角线作矩形 $A B C D, A D / / x$ 轴.反比例函数 $y = \frac{k}{x}$ 的图象经过点 $A$ .
【构建联系】

(1)、求证：函数 $y = \frac{k}{x}$ 的图象必经过点 $C$ .

(2)、如2图，把矩形ABCD沿BD折叠，点 $C$ 的对应点为 $E$ .当点 $E$ 落在 $y$ 轴上，且点 $B$ 的坐标为 $(1, 2)$ 时，求 $k$ 的值.

(3)、【深入探究】
如3图，把矩形ABCD沿BD折叠，点 $C$ 的对应点为 $E$ .当点E，A重合时，连接AC交BD于点 $P$ .以点 $O$ 为圆心，AC长为半径作 $⊙ O$ .若 $O P = 3 \sqrt{2}$ ，当 $⊙ O$ 与 $△ A B C$ 的边有交点时，求 $k$ 的取值范围.

查看试题解析