第三章 《 图形的平移与旋转》1.图形的平移(1)——北师大版数学八（下） 课堂达标测试

试卷日期：2025-01-26 考试类型：同步测试

前去【出卷网】下载

一、选择题（每题5分，共25分）

  • 1. 下列四个图案中，可用平移来分析整个图案的形成过程的图案是（       ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 如图，正方形中有一个由若干个长方形组成的对称图案，其中正方形边长是80cm ， 则图中阴影图形的周长是（ ）

    A、440cm B、320cm C、280cm D、160cm

    查看试题解析

  • 3. 如图，将△ABC沿BC方向平移1cm 得到对应的△A'B'C'．若B'C=2cm，则BC'的长是（    ）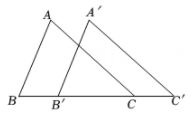

    A、2cm B、3cm C、4cm D、5cm

    查看试题解析

  • 4. 如图，将△ABC沿射线BC方向移动，使点B移动到点C ， 得到△DCE ， 连接AE ， 若△ABC的面积为2，则△ACE的面积为（    ）

      

    A、2 B、4 C、6 D、16

    查看试题解析

  • 5. 如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到△DEF的位置，AB=10,DO=4 ， 平移距离为6，则阴影部分面积为（       ）

    A、48 B、96 C、84 D、42

    查看试题解析

二、填空题（每题5分，共25分）

  • 6. 如图，将周长为8的 △ABC 沿BC边向右平移2个单位，得到 △DEF ，则四边形 ABFD 的周长为.

    查看试题解析

  • 7. 如图，在△ABC中，BC＝3，将△ABC平移5个单位长度得到△A1B1C1 ， 点P、Q分别是AB、A1C1的中点，PQ的最小值等于.

    查看试题解析

  • 8. 点 A 在数轴上距离原点2个单位长度，若有一个点从点 A 处向右移动3个单位长度，再向左移动4个单位长度，则此时该点所表示的数是.

    查看试题解析

  • 9. 如图，在长方形地块内修筑同样宽的两条“相交”的道路，余下部分作绿化，当道路宽为2米时，则绿化的面积为 平方米．

    查看试题解析

  • 10. 将Rt△ABC沿边向右平移得到Rt△DEF ， AB=8 ， BE=6 ， DG=3 ， 则阴影部分的面积为 ．


    查看试题解析

三、解答题（共5题，共50分）

  • 11. 如图，在由边长为1个单位长度的小正方形组成的网格中，点A ， B ， C ， D均为格点（网格线的交点）．

      

    (1)、画出线段AB关于直线CD对称的线段A1B1；
    (2)、将线段AB向左平移2个单位长度，再向上平移1个单位长度，得到线段A2B2 ， 画出线段A2B2；
    (3)、描出线段AB上的点M及直线CD上的点N ， 使得直线MN垂直平分AB ．

    查看试题解析

  • 12. 如图，方格纸中每个小正方形的边长均为1个单位长度，线段AB和线段CD的端点均在小正方形的顶点上．

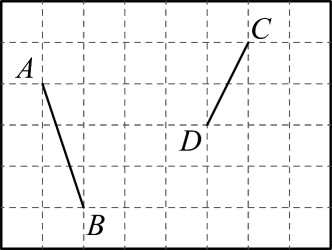    (1)、在方格纸中画出△ABE ， 且AB=BE ， ∠ABE为钝角（点E在小正方形的顶点上）；
    (2)、在方格纸中将线段CD向下平移2个单位长度，再向右平移1个单位长度后得到线段MN（点C的对应点是点M ， 点D的对应点是点N），连接EN ， 请直接写出线段EN的长．

    查看试题解析

  • 13. 如图所示，∠ACB=90°，∠A=33°，将三角形ABC沿AB方向向右平移得到三角形DEF．

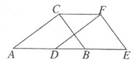    (1)、求∠E的度数；
    (2)、若AE=9cm，DB=2 cm．求CF的长度．

    查看试题解析

  • 14. 如图，ΔABC,ΔCEF都是由ΔBDE平移得到的图形，A,C,F三点在同一直线上，已知∠D=70°,∠BED=45° ．

    （1）BE=12AF成立吗？请说理由

    （2）求∠ECF的度数；

    查看试题解析

  • 15. 综合与实践

    如图．AB∥CD ， ∠B=∠ADC=114∘ ， E，F是射线BC上的动点，且满足∠CAF＝∠DAC，AE平分∠BAF．

    (1)、直线AD与BC有何位置关系？请说明理由．
    (2)、求∠CAE的度数．
    (3)、如图，将CD向右平移至C'D'处，并始终满足∠C'AF=∠D'AC' ， 是否存在某种情况，使∠AEB=∠AC'D' ． 若存在，求出此时∠AEB的度数；若不存在，请说明理由．

    查看试题解析