第2章《 二元一次方程组》2.4 二元一次方程组的应用(2)——浙教版数学七（下）课堂达标测试
试卷日期：2025-01-23 考试类型：同步测试
一、选择题（每题5分，共25分）
-
1. 同型号的甲、乙两辆车加满气体燃料后均可行驶210km，它们各自单独行驶并返回的最远距离是105km，现在它们都从A地出发，行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶，然后甲车再行驶返回A地，而乙车继续行驶，到B地后再行驶返回A地.则B地最远可距离A地（ ）A、120km B、140km C、160km D、180km2. 母亲节来临，小明去花店为妈妈准备节日礼物．已知康乃馨每支2元，百合每支3元．小明将30元钱全部用于购买这两种花（两种花都买），小明的购买方案共有（ ）A、3种 B、4种 C、5种 D、6种3. 用1块A型钢板可制成3块C型钢板和4块D型钢板；用1块B型钢板可制成5块C型钢板和2块D型钢板.现在需要58块C型钢板、40块D型钢板，问恰好用A型钢板、B型钢板各多少块？如果设用A型钢板x块，用B型钢板y块，则可列方程组为( )A、 B、 C、 D、4. 我市在落实国家“精准扶贫”政策的过程中，为某村修建一条长为400米的公路，由甲、乙两个工程队负责施工.甲工程队独立施工2天后，乙工程队加入两工程队联合施工3天后，还剩50米的工程.已知甲工程队每天比乙工程队多施工2米，求甲、乙工程队每天各施工多少米？设甲工程队每天施工 米，乙工程队每天施工 米，根据题意，所列方程组正确的是（ ）A、 B、 C、 D、5. 上学期某班的学生都是双人桌，其中 男生与女生同桌，这些女生占全班女生的 。本学期该班新转入4个男生后，男女生刚好一样多，设上学期该班有男生x人，女生y人．根根据题意可得方程组为（ ）A、 B、 C、 D、
二、填空题（每题5分，共25分）
-
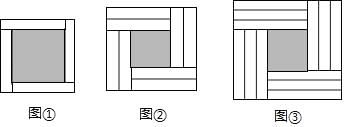
6. 端午节是中国传统节日，人们有吃粽子的习俗.某商场从6月12日起开始打折促销，肉粽六折，白粽七折，打折前购买4盒肉粽和5盒白粽需350元，打折后购买5盒肉粽和10盒白粽需360元.轩轩同学想在今天中考结束后，为敬老院送肉粽和白粽各5盒，则他6月13日购买的花费比在打折前购买节省元.7. 用若干个形状、大小完全相同的矩形纸片围成正方形，4个矩形纸片围成如图①所示的正方形，其阴影部分的面积为12；8个矩形纸片围成如图②所示的正方形，其阴影部分的面积为8；12个矩形纸片围成如图③所示的正方形，其阴影部分的面积为 ．
8. 如图，某新型休闲凳可无缝叠在一起，从而节省了收纳空间，那么高76cm的收纳柜恰好可以收纳把休闲凳。
9. 古代中国是世界中心，诸多技艺均领先世界水平，榫卯（sǔn mǎo）结构就是其中最为华丽的一点．榫卯是在两个木构件上所采用的一种凹凸结合的连接方式．已知有若干个相同的木构件，其形状如图1所示．当3个木构件紧密拼成一列时，总长度为17cm，当9个木构件紧密拼成一列时，总长度为50cm，如图2所示，则图1中的木构件长度为 ．
10. 某校七年级二班 50 名同学举办赈灾献爱心活动， 共捐出零花钱 1380 元． 捐款情况如下表：
表格中捐 20 元和 30 元的人数不小心被污染了， 看不清楚． 若设捐 20 元的有 人， 捐 30 元的有 人， 根据题意， 可列出方程组.捐款金额（元） 10 20 30 50 人数 6 ■ ■ 8 三、解答题（共5题，共50分）
-
11. 为进行某项数学综合与实践活动，小明到一个批发兼零售的商店购买所需工具．该商店规定一次性购买该工具达到一定数量后可以按批发价付款，否则按零售价付款．小明如果给学校九年级学生每人购买一个，只能按零售价付款，需用3600元；如果多购买60个，则可以按批发价付款，同样需用3600元，若按批发价购买60个与按零售价购买50个所付款相同，求这个学校九年级学生有多少人？12. 某运输公司有A、B两种货车，3辆A货车与2辆B货车一次可以运货90吨，5辆A货车与4辆B货车一次可以运货160吨.(1)、请问1辆A货车和1辆B货车一次可以分别运货多少吨?(2)、目前有190吨货物需要运输，该运输公司计划安排A、B两种货车将全部货物一次运完(A、B两种货车均满载)，其中每辆A货车一次运货花费500元，每辆B货车一次运货花费400元.请你列出所有的运输方案，并指出哪种运输方案费用最少.13. 亚洲文明对话大会召开期间，大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场，若单独调配36座新能源客车若干辆，则有2人没有座位；若只调配22座新能源客车，则用车数量将增加4辆，并空出2个座位.(1)、计划调配36座新能源客车多少辆？该大学共有多少名志愿者？(2)、若同时调配36座和22座两种车型，既保证每人有座，又保证每车不空座，则两种车型各需多少辆？14. 体育器材室有A、B两种型号的实心球，1只A型球与1只B型球的质量共7千克，3只A型球与1只B型球的质量共13千克.(1)、每只A型球、B型球的质量分别是多少千克?(2)、现有A型球、B型球的质量共17千克，则A型球、B型球各有多少只?15. 为拓展学生视野，某中学组织八年级师生开展研学活动，原计划租用45座客车若干辆，但有15人没有座位；若租用同样数量的60座客车，则多出三辆车，且其余客车恰好坐满．现有甲、乙两种客车，它们的载客量和租金如下表所示：
甲型客车
乙型客车
载客量（人/辆）
45
60
租金（元/辆）
200
300
(1)、参加此次研学活动的师生人数是多少？原计划租用多少辆45座客车？(2)、若租用同一种客车，要使每位师生都有座位，应该怎样租用才合算？