北师大版数学八年级上学期期末模拟卷(三)
试卷日期:2024-12-16 考试类型:期末考试
一、选择题(每题3分,共36分)
-
1. 已知实数 , 满足 , 且 , 则的值为( )A、 B、 C、 D、2. 一副直角三角板按如图所示的方式摆放,点E在AB的延长线上,当DF∥AB时,∠EDB的度数为( )
 A、10° B、15° C、30° D、45°3. 下列计算正确的是( )A、 B、 C、 D、4. 某校开展了红色经典故事演讲比赛,其中名同学的成绩单位:分分别为: , , , , , , , 关于这组数据,下列说法中正确的是( )A、众数是 B、中位数是 C、平均数是 D、方差是5. 对于一次函数 , 下列结论正确的是( )A、它的图象与轴交于点 B、随的增大而减小 C、当时, D、它的图象经过第一、二、三象限6. 如图,在中, , 是内一点,且 , , 则的度数是( )
A、10° B、15° C、30° D、45°3. 下列计算正确的是( )A、 B、 C、 D、4. 某校开展了红色经典故事演讲比赛,其中名同学的成绩单位:分分别为: , , , , , , , 关于这组数据,下列说法中正确的是( )A、众数是 B、中位数是 C、平均数是 D、方差是5. 对于一次函数 , 下列结论正确的是( )A、它的图象与轴交于点 B、随的增大而减小 C、当时, D、它的图象经过第一、二、三象限6. 如图,在中, , 是内一点,且 , , 则的度数是( ) A、 B、 C、 D、7. 某班七个合作学习小组人数如下:5,5,6, , 6,7,8,已知这组数据的平均数为6,则这组数据的中位数和众数是( )A、6,5 B、6,6 C、和6 D、和68. 已知 , 则实数m的范围是( )A、 B、 C、 D、9. 点在直线上,坐标是二元一次方程的解,则点P的位置在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 将含角的直角三角板按如图方式摆放,已知 , , 则( )
A、 B、 C、 D、7. 某班七个合作学习小组人数如下:5,5,6, , 6,7,8,已知这组数据的平均数为6,则这组数据的中位数和众数是( )A、6,5 B、6,6 C、和6 D、和68. 已知 , 则实数m的范围是( )A、 B、 C、 D、9. 点在直线上,坐标是二元一次方程的解,则点P的位置在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限10. 将含角的直角三角板按如图方式摆放,已知 , , 则( )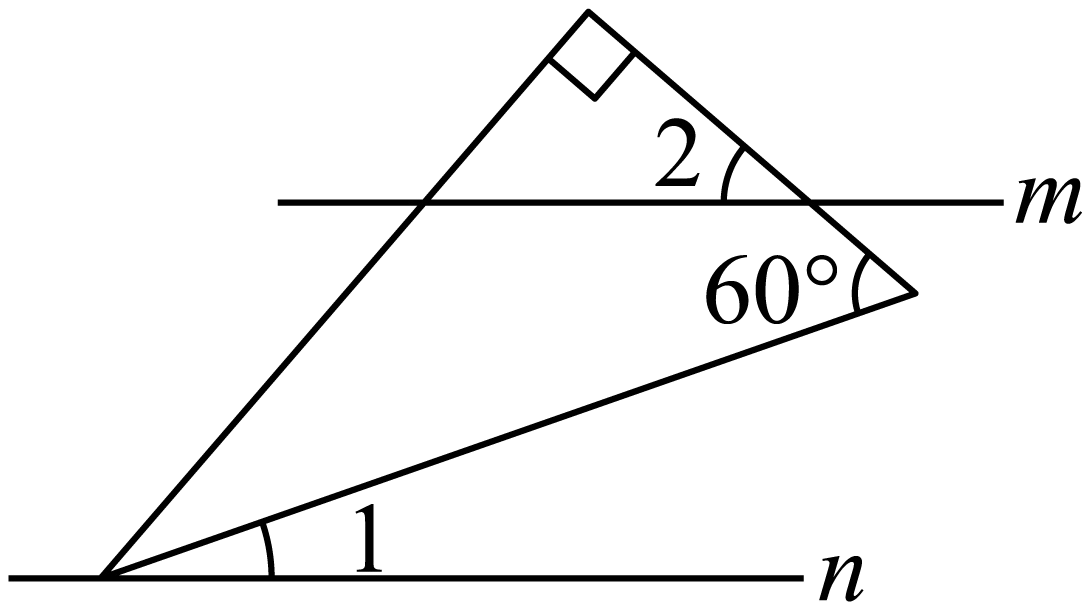 A、 B、 C、 D、11. 如图,将三角形纸片沿折叠,点落在点处,已知 , 则的度数为( )
A、 B、 C、 D、11. 如图,将三角形纸片沿折叠,点落在点处,已知 , 则的度数为( ) A、 B、 C、 D、以上都不对12. 如图,在平面直角坐标系中,直线:与直线:交于点 , 则关于、的方程组的解为( )
A、 B、 C、 D、以上都不对12. 如图,在平面直角坐标系中,直线:与直线:交于点 , 则关于、的方程组的解为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
13. 如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是;点B表示的数是 .
 14. 观察下列运算过程:
14. 观察下列运算过程:……
请运用上面的运算方法计算:
= .
15. 《九章算术》中记载了一道数学问题,其译文为:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛(斛,音hú,是古代一种容量单位),1个大桶加上5个小桶可以盛酒2斛.1个大桶、1个小桶分别可以盛酒多少斛?设1个大桶可以盛酒斛、1个小桶可以盛酒斛.根据题意,可列方程组为 .16. 如图,在△ABC中,∠B=50°,∠C=30°,AD是高,以点A为圆心,AB长为半径画弧,交AC于点E , 再分别以B、E为圆心,大于BE的长为半径画弧,两弧在∠BAC的内部交于点F , 作射线AF , 则∠DAF=°. 17. 如图,Rt△ABC中,∠C=90°,AC=8,BC=4,折叠△ABC , 使点A与点B重合,折痕DE与AB交于点D , 与AC交于点E , 则CE的长为.
17. 如图,Rt△ABC中,∠C=90°,AC=8,BC=4,折叠△ABC , 使点A与点B重合,折痕DE与AB交于点D , 与AC交于点E , 则CE的长为. 18. 如图,在平面直角坐标系中,直线y=﹣ x+4与x轴、y轴分别交于A、B两点,点C在第二象限,若BC=OC=OA,则点C的坐标为.
18. 如图,在平面直角坐标系中,直线y=﹣ x+4与x轴、y轴分别交于A、B两点,点C在第二象限,若BC=OC=OA,则点C的坐标为.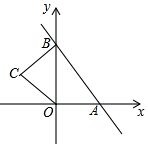
三、解答题(共7题,共66分)
-
19. 计算:(1)、;(2)、 .20. 计算:(1)、(2)、21. 如图,在中, , 平分 , 交于点F.
 (1)、若 , , 求的度数;(2)、在(1)的条件下,判断与是否垂直,并说明理由;(3)、直接写出当与满足怎样的数量关系时, .22. 在某购物电商平台上,客户购买商家的商品后,可从“产品质量”“商家服务”“发货速度”“快递服务”等方面给予商家分值评价(分值为1分、2分、3分、4分和5分).该平台上甲、乙两个商家以相同价格分别销售同款T恤衫,平台为了了解他们的客户对其“商家服务”的评价情况,从甲、乙两个商家各随机抽取了一部分“商家服务”的评价分值进行统计分析.(1)、【数据描述】
(1)、若 , , 求的度数;(2)、在(1)的条件下,判断与是否垂直,并说明理由;(3)、直接写出当与满足怎样的数量关系时, .22. 在某购物电商平台上,客户购买商家的商品后,可从“产品质量”“商家服务”“发货速度”“快递服务”等方面给予商家分值评价(分值为1分、2分、3分、4分和5分).该平台上甲、乙两个商家以相同价格分别销售同款T恤衫,平台为了了解他们的客户对其“商家服务”的评价情况,从甲、乙两个商家各随机抽取了一部分“商家服务”的评价分值进行统计分析.(1)、【数据描述】如图是根据样本数据制作的不完整的统计图,请回答下列问题.

①平台从甲、乙两个商家分别抽取了多少个评价分值?请补全条形统计图;
②求甲商家的“商家服务”评价分值的扇形统计图中圆心角α的度数.
(2)、【分析与应用】样本数据的统计量如下表,请回答下列问题.
商家
统计量
中位数
众数
平均数
方差
甲商家
a
3
3.5
1.05
乙商家
4
b
1.24
①直接写出表中a和b的值,并求的值;
②小亮打算从甲、乙两个商家中选择“商家服务”好的一家购买此款T恤衫.你认为小亮应该选择哪一家?说明你的观点.
23. 为迎接“创文创卫活动”,某市环卫局准备购买A、B两种型号的垃圾箱,买2个A型垃圾箱和1个B型垃圾箱共需100元;买1个A型垃圾箱和3个B型垃圾箱共需150元.(1)、每个A型垃圾箱和B型垃圾箱各多少元?(2)、购买A、B两种型号的垃圾箱共50个,其中A型垃圾箱a(0≤a≤16)个,求购买垃圾箱的总费用w(元)与A型垃圾箱a(个)之间的函数关系式,并说明总费用最少需要多少元?

