北师大版数学八年级上学期期末模拟卷(二)
试卷日期:2024-12-11 考试类型:期末考试
一、选择题(每题3分,共36分)
-
1. 如图, , , , 则的度数为( )
 A、 B、 C、 D、2. 射击运动队进行射击测试,甲、乙两名选手的测试成绩如图,其成绩的方差分别记为S甲2和S乙2 , 则S甲2和S乙2的大小关系是( )
A、 B、 C、 D、2. 射击运动队进行射击测试,甲、乙两名选手的测试成绩如图,其成绩的方差分别记为S甲2和S乙2 , 则S甲2和S乙2的大小关系是( )≈
 A、S甲2>S乙2 B、S甲2<S乙2 C、S甲2=S乙2 D、无法确定3. 估计的值应在( )A、8和9之间 B、9和10之间 C、10和11之间 D、11和12之间4. 若一次函数y=kx+3的函数值y随x的增大而增大,则k的值可以是( )A、-2 B、-1 C、0 D、15. 如图,矩形中,对角线的垂直平分线分别交 , 于点 , 若 , , 则的长为( )
A、S甲2>S乙2 B、S甲2<S乙2 C、S甲2=S乙2 D、无法确定3. 估计的值应在( )A、8和9之间 B、9和10之间 C、10和11之间 D、11和12之间4. 若一次函数y=kx+3的函数值y随x的增大而增大,则k的值可以是( )A、-2 B、-1 C、0 D、15. 如图,矩形中,对角线的垂直平分线分别交 , 于点 , 若 , , 则的长为( )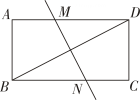 A、 B、 C、 D、6. 若一组数据1,2,4,3, , 0的平均数是2,则众数是( )A、1 B、2 C、3 D、47. 设 的整数部分为a , 小数部分为b , 则 的值是( )A、6 B、 C、12 D、8. 若方程组的解中 , 则等于( )A、2024 B、2025 C、2026 D、20279. 甲、乙两人沿相同路线由A地到B地匀速前进,两地之间的路程为20km . 两人前进路程s(单位:km)与甲的前进时间t(单位:h)之间的对应关系如图所示.根据图象信息,下列说法正确的是( )
A、 B、 C、 D、6. 若一组数据1,2,4,3, , 0的平均数是2,则众数是( )A、1 B、2 C、3 D、47. 设 的整数部分为a , 小数部分为b , 则 的值是( )A、6 B、 C、12 D、8. 若方程组的解中 , 则等于( )A、2024 B、2025 C、2026 D、20279. 甲、乙两人沿相同路线由A地到B地匀速前进,两地之间的路程为20km . 两人前进路程s(单位:km)与甲的前进时间t(单位:h)之间的对应关系如图所示.根据图象信息,下列说法正确的是( ) A、甲比乙晚出发1h B、乙全程共用2h C、乙比甲早到B地3h D、甲的速度是5km/h10. 将一副三角尺如图摆放,使有刻度的两条边互相平行,则的大小为( )
A、甲比乙晚出发1h B、乙全程共用2h C、乙比甲早到B地3h D、甲的速度是5km/h10. 将一副三角尺如图摆放,使有刻度的两条边互相平行,则的大小为( ) A、 B、 C、 D、11. 如图,在平面直角坐标系中,直线l1的解析式为y=﹣x,直线l2与l1交于B(a,﹣a),与y轴交于点A(0,b).其中a、b满足(a+2)2+=0,那么,下列说法:
A、 B、 C、 D、11. 如图,在平面直角坐标系中,直线l1的解析式为y=﹣x,直线l2与l1交于B(a,﹣a),与y轴交于点A(0,b).其中a、b满足(a+2)2+=0,那么,下列说法:(1)B点坐标是(﹣2,2);
(2)三角形ABO的面积是3;
(3) ;
(4)当P的坐标是(﹣2,5)时,那么, , 正确的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题3分,共18分)
-
12. 若 的整数部分为a,小数部分为b,则代数式 的值是.13. 计算: .14. 我国古代数学名著《张丘建算经》中有这样一题:一只公鸡值5钱,一只母鸡值3钱,3只小鸡值1钱,现花100钱买了100只鸡.若公鸡有8只,设母鸡有x只,小鸡有y只,可列方程组为。15. 如图,△ABC中,∠BCD=30°,∠ACB=80°,CD是边AB上的高,AE是∠CAB的平分线,则∠AEB的度数是 .
 16. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=4,D是边AC的中点,E是边BC上一点,连接BD、DE . 将△CDE沿DE翻折,点C落在BD上的点F处,则CE= .
16. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=4,D是边AC的中点,E是边BC上一点,连接BD、DE . 将△CDE沿DE翻折,点C落在BD上的点F处,则CE= . 17. 如图,一次函数y=kx+b的图象经过A(3,6)、B(0,3)两点,交x轴于点C , 则△AOC的面积为 .
17. 如图,一次函数y=kx+b的图象经过A(3,6)、B(0,3)两点,交x轴于点C , 则△AOC的面积为 .
三、解答题(共9题,共66分)
-
18. 计算:.19. 计算: .20. 解方程组:21. 解方程组:22. 已知:如图,点A、B、C、D在同一条直线上,AE∥BF,AE=BF.

若 ▲ , 则AB=CD.
请从①CE∥DF;②CE=DF;③∠E=∠F这3个选项中选择一个作为条件(写序号),使结论成立,并说明理由.
23. 为了解学生物理实验操作情况,随机抽取小青和小海两名同学的10次实验得分,并对他们的得分情况从以下两方面整理描述如下:①操作规范性:

②书写准确性:
小青:1 1 2 2 2 3 1 3 2 1
小海:1 2 2 3 3 3 2 1 2 1
操作规范性和书写准确性的得分统计表:
项目
统计量
学生
操作规范性
书写准确性
平均数
方差
平均数
中位数
小青
4
1.8
a
小海
4
b
2
根据以上信息,回答下列问题:
(1)、表格中的 , 比较和的大小;(2)、计算表格中b的值;(3)、综合上表的统计量,请你对两名同学的得分进行评价并说明理由;(4)、为了取得更好的成绩,你认为在实验过程中还应该注意哪些方面?24. 河南信阳毛尖是中国十大名茶之一,因其成品紧密如尖故名毛尖.某公司采购员到信阳茶叶市场购买某品牌毛尖茶,商家推出了两种购买方式:会员卡费用(元/张)
茶叶价格(元/kg)
方式一:金卡会员
500
1600
方式二:银卡会员
200
1800
设该公司此次购买茶叶xkg , 按方式一购买茶叶的总费用为y1元,按方式二购买茶叶的总费用为y2元.
(1)、请直接写出y1 , y2关于x的函数解析式;(2)、若按方式一购买茶叶的总费用和按方式二购买茶叶的总费用相同,求该公司此次购买茶叶的质量;(3)、若该公司此次购买茶叶的总预算为6500元,则按哪种方式购买可以获得更多的茶叶?25. 如图,直线与x轴交于点 , 与y轴交于点B,点C是的中点. (1)、求出点B、点C的坐标及b的值;(2)、在y轴上存在点D,使得 , 求点D的坐标;(3)、在x轴上是否存在一点P,使得是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.26. 在等腰 中, ,点D,E在射线 上, ,过点E作 ,交射线 于点F.请解答下列问题:
(1)、求出点B、点C的坐标及b的值;(2)、在y轴上存在点D,使得 , 求点D的坐标;(3)、在x轴上是否存在一点P,使得是直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.26. 在等腰 中, ,点D,E在射线 上, ,过点E作 ,交射线 于点F.请解答下列问题: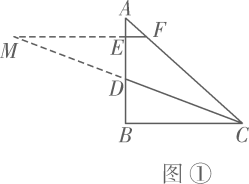
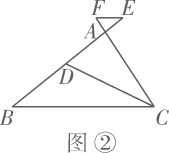
 (1)、当点E在线段 上, 是 的角平分线时,如图①,求证: ;(提示:延长 , 交于点M.)(2)、当点E在线段 的延长线上, 是 的角平分线时,如图②;当点E在线段 的延长线上, 是 的外角平分线时,如图③,请直接写出线段 , , 之间的数量关系,不需要证明;(3)、在(1)、(2)的条件下,若 ,则 .
(1)、当点E在线段 上, 是 的角平分线时,如图①,求证: ;(提示:延长 , 交于点M.)(2)、当点E在线段 的延长线上, 是 的角平分线时,如图②;当点E在线段 的延长线上, 是 的外角平分线时,如图③,请直接写出线段 , , 之间的数量关系,不需要证明;(3)、在(1)、(2)的条件下,若 ,则 .