北师大版数学八年级上学期期末模拟卷（一）

试卷日期：2024-12-10 考试类型：期末考试

前去【出卷网】下载

一、选择题（每题3分，共36分）

1. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{2} \times \sqrt{5} = \sqrt{10}$ C、 $2 \div \sqrt{2} = 1$ D、 $\sqrt{(- 5)^{2}} = - 5$

查看试题解析
2. 在平面直角坐标系中，点P(-1，m²+1)位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 某跳远队准备从甲、乙、丙、丁4名运动员中选取1名成绩优异且发挥稳定的运动员参加比赛，他们成绩的平均数和方差如下： $\bar{x_{甲}} = \bar{x_{丁}} = 5.75, \bar{x_{乙}} = \bar{x_{丙}} = 6.15,$ $S_{甲}^{2} = S_{丙}^{2} = 0.02, S_{乙}^{2} = S_{丁}^{2} = 0.45$ ，则应选择的运动员是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 如图，直线a∥b ，矩形ABCD的顶点A在直线b上，若∠2＝41°，则∠1的度数为（）

A、41° B、51° C、49° D、59°

查看试题解析
5. 如图，在平面直角坐标系中，直线 $y = 2 x + b$ 与直线 $y = - 3 x + 6$ 相交于点A，则关于x，y的二元一次方程组 ${\begin{array}{l} y = 2 x + b \\ y = - 3 x + 6 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 2 \\ y = 0 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ C、 ${\begin{matrix} x = - 1 \\ y = 9 \end{matrix}$ D、 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$

查看试题解析
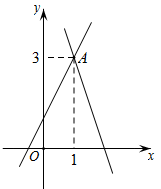6. 小明同学在计算出8个数的平均数后，不小心将这个数也混到数据中了，那么重新计算这些新数据后一定不变的量是 $($ $)$

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
7. “今有方池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐．问：水深几何？”这是我国数学史上的“葭生池中”问题．即AC＝5，DC＝1，BD＝BA ，则BC＝（）

A、8 B、10 C、12 D、13

查看试题解析
8. 为提高学生学习兴趣，增强动手实践能力，某校为物理兴趣小组的同学购买了一根长度为150cm的导线，将其全部截成10cm和20cm两种长度的导线用于实验操作（每种长度的导线至少一根），则截取方案共有（）

A、5种 B、6种 C、7种 D、8种

查看试题解析
9. 同一条公路连接A ， B ， C三地，B地在A ， C两地之间．甲、乙两车分别从A地、B地同时出发前往C地．甲车速度始终保持不变，乙车中途休息一段时间，继续行驶．如图表示甲、乙两车之间的距离y（km）与时间x（h）的函数关系．下列结论正确的是（）

A、甲车行驶 $\frac{8}{3}$ h与乙车相遇 B、A ， C两地相距220km C、甲车的速度是70km/h D、乙车中途休息36分钟

查看试题解析
10. 如图，在同一平面直角坐标系中，一次函数 $y = k_{1} x + b_{1}$ 与 $y = k_{2} x + b_{2}$ （其中 $k_{1} k_{2} \neq 0$ ， $k_{1}$ ， $k_{2}$ ， $b_{1}$ ， $b_{2}$ 为常数）的图象分别为直线 $l_{1}$ ， $l_{2}$ .下列结论正确的是（）

A、 $b_{1} + b_{2} > 0$ B、 $b_{1} b_{2} > 0$ C、 $k_{1} + k_{2} < 0$ D、 $k_{1} k_{2} < 0$

查看试题解析
11. 如图， $△ A B C$ 中， $∠ B A C = 55 °$ ，将 $△ A B C$ 逆时针旋转 $α (0 ° < α < 55 °) ，$ 得到 $△ A D E$ ， $D E$ 交 $A C$ 于F．当 $α = 40 °$ 时，点D恰好落在 $B C$ 上，此时 $∠ A F E$ 等于（）

A、 $80 °$ B、 $85 °$ C、 $90 °$ D、 $95 °$

查看试题解析
12. 如图，三角形纸片ABC中，∠BAC＝90°，AB＝2，AC＝3．沿过点A的直线将纸片折叠，使点B落在边BC上的点D处；再折叠纸片，使点C与点D重合，若折痕与AC的交点为E，则AE的长是（）

A、 $\frac{13}{6}$ B、 $\frac{5}{6}$ C、 $\frac{7}{6}$ D、 $\frac{6}{5}$

查看试题解析

二、填空题（每题3分，共18分）

13. 若关于x、y的二元一次方程组 $\{\begin{array}{l} a x + y = b \\ c x - y = d \end{array}$ 的解是 $\{\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ ，则关于x、y的方程组 $\{\begin{array}{l} a x + 2 y = 2 a + b \\ c x - 2 y = 2 c + d \end{array}$ 的解是．

查看试题解析
14. 在平面直角坐标系中，已知点 $P (a ， 1)$ 与点 $Q (2 ， b)$ 关于 $x$ 轴对称，则 $a + b =$ ．

查看试题解析
15. 如图，在△ABC中，AE₁ ， BE₁分别是内角∠CAB ，外角∠CBD的三等分线，且∠E₁AD＝ $\frac{1}{3}$ ∠CAB ， ∠E₁BD＝ $\frac{1}{3}$ ∠CBD ，在△ABE₁中，AE₂ ， BE₂分别是内角∠E₁AB ，外角∠E₁BD的三等分线，且∠E₂AD＝ $\frac{1}{3}$ ∠E₁AB ， ∠E₂BD＝ $\frac{1}{3}$ ∠E₁BD ， …，以此规律作下去，若∠C＝m°，则∠E_n＝度．

查看试题解析
16. 若关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} 2 x - y = k - 2 \\ 2 y - x = 1 \end{array}$ 的解满足 $x + y = 2021$ ，则 $k =$ .

查看试题解析
17. 人们把 $\frac{\sqrt{5} - 1}{2}$ 这个数叫做黄金分割数，著名数学家华罗庚优选法中的 $0.618$ 法就应用了黄金分割数.设 $a = \frac{\sqrt{5} - 1}{2}$ ， $b = \frac{\sqrt{5} + 1}{2}$ ，则 $a b = 1$ ，记 $S_{1} = \frac{1}{1 + a} + \frac{1}{1 + b}$ ， $S_{2} = \frac{1}{1 + a^{2}} + \frac{1}{1 + b^{2}}$ ，…， $S_{10} = \frac{1}{1 + a^{10}} + \frac{1}{1 + b^{10}}$ .则 $S_{1} + S_{2} + \dots + S_{10} =$ .

查看试题解析
18. 已知x，y是实数，且满足y= $\sqrt{x - 2}$ ＋ $\sqrt{2 - x}$ ＋ $\frac{1}{8}$ ，则 $\sqrt{x} \cdot \sqrt{y}$ 的值是．

查看试题解析

三、解答题（共9题，共66分）

19. 计算 $| - \sqrt{2} | + {(\sqrt{2} - \frac{1}{2})}^{2} - {(\sqrt{2} + \frac{1}{2})}^{2}$ ．

查看试题解析
20. 解方程组： ${\begin{cases} 2 x - y = 5 \\ 4 x + 3 y = - 10 \end{cases}$ ．

查看试题解析
21. 解方程组： ${\begin{array}{l} x - 2 y = 3 \\ \frac{1}{2} x + \frac{3}{4} y = \frac{13}{4} \end{array}$

查看试题解析
22. 为激发青少年崇尚科学、探索未知的热情，学校开展“科学小博士”知识竞赛。各班以小组为单位组织初赛，规定满分为10分，9分及以上为优秀．
数据整理：小夏将本班甲、乙两组同学（每组8人）初赛的成绩整理成如下的统计图．
数据分析：小夏对这两个小组的成绩进行了如下分析：

平均数（分）
中位数（分）
众数（分）
方差
优秀率
甲组
7.625
a
7
4.48
37.5%
乙组
7.625
7
b
0.73
c
请认真阅读上述信息，回答下列问题：

(1)、填空： $a =$ ， $b =$ ， $c =$ ；

(2)、小祺认为甲、乙两组成绩的平均数相等，因此两个组成绩一样好．小夏认为小祺的观点比较片面，请结合上表中的信息帮小夏说明理由（写出两条即可）．

查看试题解析
23. 甲、乙两货车分别从相距225km的A、B两地同时出发，甲货车从A地出发途经配货站时，停下来卸货，半小时后继续驶往B地，乙货车沿同一条公路从B地驶往A地，但乙货车到达配货站时接到紧急任务立即原路原速返回B地，结果比甲货车晚半小时到达B地．如图是甲、乙两货车距A地的距离y（km）与行驶时间x（h）之间的函数图象，结合图象回答下列问题：

(1)、甲货车到达配货站之前的速度是km/h ，乙货车的速度是km/h；

(2)、求甲货车在配货站卸货后驶往B地的过程中，甲货车距A地的距离y（km）与行驶时间x（h）之间的函数解析式；

(3)、直接写出甲、乙两货车在行驶的过程中，出发多长时间甲、乙两货车与配货站的距离相等．

查看试题解析
24. 如图，点 $A$ ， $D$ ， $C$ ， $F$ 在同一条直线上， $AB = DE$ ， $BC = EF .$ 有下列三个条件： $① AC = DF$ ， $② ∠ ABC = ∠ DEF$ ， $③ ∠ ACB = ∠ DFE$ ．

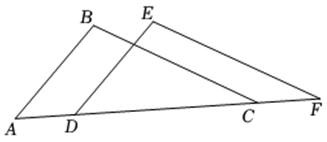(1)、请在上述三个条件中选取一个条件，使得 $△ ABC$ ≌ $△ DEF$ ．
你选取的条件为 ( 填写序号 ) ( 只需选一个条件，多选不得分 )，你判定 $△ ABC$ ≌ $△ DEF$ 的依据是 (填“ $SSS$ ”或“ $SAS$ ”或“ $ASA$ ”或“ $AAS$ ”)；

(2)、利用 $(1)$ 的结论 $△ ABC$ ≌ $△ DEF .$ 求证： $AB / / DE$ ．

查看试题解析
25. 如图，已知过点 $B (1 ， 0)$ 的直线 $l_{1}$ 与直线 $l_{2}$ ： $y = 2 x + 4$ 相交于点 $P (- 1 ， a)$ .

(1)、求直线 $l_{1}$ 的解析式；

(2)、求四边形 $P A O C$ 的面积.

查看试题解析
26. 某商场购进A，B两种商品，已知购进3件A商品和5件B商品费用相同，购进3件A商品和1件B商品总费用为360元.

(1)、求A，B两种商品每件进价各为多少元？（列方程或方程组求解）

(2)、若该商场计划购进A，B两种商品共80件，其中A商品m件.若A商品按每件150元销售，B商品按每件80元销售，求销售完A，B两种商品后获得总利润w（元）与m（件）的函数关系式.

查看试题解析

	平均数（分）	中位数（分）	众数（分）	方差	优秀率
甲组	7.625	a	7	4.48	37.5%
乙组	7.625	7	b	0.73	c