【提升版】北师大版数学八年级上册第五章二元一次方程组章节测试卷

试卷日期：2024-12-01 考试类型：单元试卷

前去【出卷网】下载

一、选择题（每题3分，共24分）

1. 已知方程组 ${\begin{array}{l} x + 2 y = 4 \\ 2 x + y = k \end{array}$ 的解满足 $x + y = 1$ ，则 $k$ 的值为（）

A、7 B、 $- 7$ C、1 D、 $- 1$

查看试题解析
2. 若满足方程组 ${\begin{cases} 3 x + y = m + 3 \\ 2 x - y = 2 m - 1 \end{cases}$ 的 $x$ 与 $y$ 互为相反数，则 $m$ 的值为（）

A、11 B、-1 C、1 D、-11

查看试题解析
3. 《孙子算经》中有一道题，原文是：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余4.5尺；将绳子对折再量长木，长木还剩余l尺，问木长多少尺？若设木长 $x$ 尺，绳子长 $y$ 尺，则可列方程组为（）

A、 ${\begin{array}{l} y - x = 4.5 \\ x - 2 y = 1 \end{array}$ B、 ${\begin{array}{l} x - y = 4.5 \\ 2 y - x = 1 \end{array}$ C、 ${\begin{array}{l} y - x = 4.5 \\ x - \frac{1}{2} y = 1 \end{array}$ D、 ${\begin{array}{l} x - y = 4.5 \\ \frac{1}{2} y - x = 1 \end{array}$

查看试题解析
4. $《$ 九章算术 $》$ 是人类科学史上应用数学的“算经之首”，其书中卷八方程 $[$ 七 $]$ 中记载“今有牛五、羊二，直金十两 $.$ 牛二、羊五，直金八两 $.$ 牛、羊各直金几何？”题目大意是：“ $5$ 头牛、 $2$ 只羊共值金 $10$ 两 $. 2$ 头牛、 $5$ 只羊共值金 $8$ 两，每头牛、每只羊各值金多少两？”设每头牛值金 $x$ 两，每只羊值金 $y$ 两，那么下面列出的方程组中正确的是（）

A、 ${\begin{array}{l} 5 x + 2 y = 10 \\ 2 x + 5 y = 8 \end{array}$ B、 ${\begin{array}{l} x + y = 8 \\ 2 x + 5 y = 10 \end{array}$ C、 ${\begin{array}{l} 5 x + 2 y = 8 \\ x + y = 10 \end{array}$ D、 ${\begin{array}{l} 5 x + 2 y = 8 \\ 2 x + 5 y = 10 \end{array}$

查看试题解析
5. 已知方程组 ${\begin{matrix} 5 x + y = 3 \\ a x + 5 y = 4 \end{matrix}$ 和 ${\begin{matrix} x - 2 y = 5 \\ 5 x + b y = 1 \end{matrix}$ 有相同的解，则a，b的值为（）

A、 ${\begin{matrix} a = 14 \\ b = 2 \end{matrix}$ B、 ${\begin{matrix} a = 4 \\ b = - 6 \end{matrix}$ C、 ${\begin{matrix} a = - 6 \\ b = 2 \end{matrix}$ D、 ${\begin{matrix} a = 1 \\ b = 2 \end{matrix}$

查看试题解析
6. 若方程组 $\{\begin{array}{l} 3 x - y = 4 k - 5 \\ 2 x + 6 y = k \end{array}$ 的解中 $x + y = 2024$ ，则 $k$ 等于（）

A、2024 B、2025 C、2026 D、2027

查看试题解析
7. 若二元一次联立方程式 $\{\begin{array}{l} 5 x - 3 y = 28 \\ y = - 3 x \end{array}$ 的解为 $\{\begin{array}{l} x = a \\ y = b \end{array}$ ，则 $a + b$ 之值为何？（　　）

A、 $- 28$ B、 $- 14$ C、 $- 4$ D、14

查看试题解析
8. 我国明代数学家程大位所著《算法统宗》中记载了一道有趣的题目：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”题目大意是：100个和尚分100个馒头，刚好分完．大和尚1人分3个馒头，小和尚3人分一个馒头．问大、小和尚各有多少人？若大和尚有x人，小和尚有y人．则下列方程或方程组中，正确的有（）
① ${\begin{array}{l} x + y = 100 \\ \frac{1}{3} x + 3 y = 100 \end{array}$ ；② ${\begin{array}{l} x + y = 100 \\ 3 x + \frac{1}{3} y = 100 \end{array}$ ；③3x+ $\frac{1}{3}$ （100-x）＝100；④ $\frac{1}{3}$ y+3（100-y）＝100．

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题（每题3分，共15分）

9. 如图，函数 $y = a x + b$ 和 $y = - \frac{1}{3} x$ 的图象相交于点P ，则关于x ， y的二元一次方程组 ${\begin{array}{l} - a x + y = b \\ x + 3 y = 0 \end{array}$ 的解是．

查看试题解析
10. 若一次函数 $y = k_{1} x + b_{1}$ 与 $y = k_{2} x + b_{2}$ 的图象相交于点 $(2，3)$ ，则方程组 $\{\begin{array}{l} y = k_{1} x + b_{1} \\ y = k_{2} x + b_{2} \end{array}$ 的解是．

查看试题解析
11. 若关于x、y的二元一次方程组 ${\begin{array}{l} 3 x - m y = 5 \\ 2 x + n y = 6 \end{array}$ 的解是 ${\begin{cases} x = 2 \\ y = 4 \end{cases}$ ，则关于a、b的二元一次方程组 ${\begin{array}{l} 3 (a + b) - m (a - b) = 5 \\ 2 (a + b) + n (a - b) = 6 \end{array}$ 的解是．

查看试题解析
12. 数形结合是解决数学问题常用的思想方法，如图，直线 $y = x + 5$ 和直线 $y = a x + b$ 相交于点P，根据图象可知，方程组 ${\begin{array}{l} x - y + 5 = 0 \\ a x - y + b = 0 \end{array}$ 的解是．

查看试题解析
13. 一个两位数m的十位上的数字是a，个位上的数字是b，记 $f (m) = a + b$ 为这个两位数m的“衍生数”．如 $f (49) = 4 + 9 = 13$ ．现有2个两位数x和y，且满足 $x + y = 100$ ，则 $f (x) + f (y) =$ ．

查看试题解析

三、解答题（共7题，共61分）

14. 解方程组

(1)、 $\{\begin{array}{l} x + y = 7 \\ 3 x + y = 17 \end{array}$

(2)、 $\{\begin{array}{l} 2 x + 3 y - z = 18 \\ 3 x - 2 y + z = 8 \\ x + 2 y + z = 24 \end{array}$

查看试题解析
15. 某商场第1次用39万元购进A，B两种商品，销售完后获得利润6万元，它们的进价和售价如表（总利润＝单件利润×销售量）：
价格
商品
进价（元/件）
售价（元/件）
A
1200
1350
B
1000
1200

(1)、该商场第1次购进A，B两种商品各多少件？

(2)、商场第2次以原进价购进A，B两种商品，购进A商品的件数不变，而购进B商品的件数是第1次的2倍，A商品按原售价销售，而B商品打折销售，若两种商品销售完毕，要使得第2次经营活动获得利润等于5.4万元，则B种商品是按几折销售的？

查看试题解析
16. 如图，在平面直角坐标系中，点A（2，2），点B（-4，0），直线AB交y轴于点C．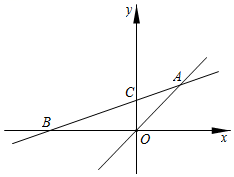

(1)、求直线AB的表达式和点C的坐标；

(2)、在直线OA上有一点P，使得△BCP的面积为4，求点P的坐标．

查看试题解析
17. 某校为了做好大课间活动，计划用400元购买10件体育用品，备选体育用品及单价如下表（单位：元）
备用体育用品
篮球
排球
羽毛球拍
单位（元）
50
40
25
（1）若400元全部用来购买篮球和羽毛球拍共10件，问篮球和羽毛球拍各购买多少件？
（2）若400元全部用来购买篮球、排球和羽毛球拍三种共10件，能实现吗？若能，求出篮球、排球、羽毛球拍各购买多少件；若不能，请说明理由．

查看试题解析
18. 阅读材料并回答下列问题：
当 $m, n$ 都是实数，且满足 $m - n = 6$ ，就称点 $P (m - 1,3 n + 1)$ 为"友好点". 例如：点 $E (3,1)$ ，令 $\{\begin{array}{l} m - 1 = 3 \\ 3 n + 1 = 1 \end{array}$ ，得 $\{\begin{array}{l} m = 4 \\ n = 0 \end{array}, m - n = 4 \neq 6$ ，所以 $E (3,1)$ 不是"友好点"，点 $P (4, - 2)$ ，令 $\{\begin{array}{l} m - 1 = 4 \\ 3 n + 1 = - 2 \end{array}$ .
得 $\{\begin{array}{l} m = 5 \\ n = - 1 \end{array}, m - n = 6$ ，所以 $F (4, - 2)$ 是"友好点".

(1)、请判断点 $A (7,1), B (6,4)$ 是否为"友好点"，并说明理由.

(2)、以关于 $x, y$ 的方程组 $\{\begin{array}{l} x + y = 2 \\ 2 x - y = t \end{array}$ 的解为坐标的点 $C (x, y)$ 是 "友好点"，求t 的值.

查看试题解析
19. 由于连日大雨，某城市局部面临内涝，当地相关部门迅速组织防涝抗涝工作，抽调一批抽水泵紧急抽水排险．经在抽水现场测得A型和B型两款抽水泵抽水量情况如下：4台A型抽水泵和5台B型抽水泵同时工作 $20 \min$ ，可抽水 $300 m^{3}$ 的水；2台A型抽水泵和10台B型抽水泵同时工作 $10 \min$ ，可抽水 $210 m^{3}$ 的水．

(1)、求A、B两款抽水泵每分钟分别能抽水多少立方米？

(2)、该地防洪相关部门，为了以后抗涝需要，计划进购一批A型和B型两款抽水泵，要求这批抽水泵全部同时工作1分钟，能抽水150立方米的水．设购买A型抽水泵m台，B型抽水泵 $n (20 \leq n \leq 50)$ 台，请用含n的代数式表示m．

(3)、A型抽水泵每台标价2万元，若一次性购买不少于30台，可打九折，若少于30台则按标价销售；B型抽水泵每台标价3万元，若一次性购买不少于30台，可打八折，若少于30台则也按标价销售；在（2）的条件下，问如何购买使得总费用最小？请通过分析计算给予说明．

查看试题解析
20. 如图（a）所示，在平面直角坐标系中，直线 $y = \frac{1}{2} x - 2$ 与 $x$ 轴、 $y$ 轴分别交于 $A$ ， $B$ 两点，直线 $y = - x + b$ 经过点 $A$ ，并与 $y$ 轴交于点 $C$ ．

(1)、求 $A$ ， $B$ 两点的坐标及 $b$ 的值；

(2)、如图（b）所示，动点 $P$ 从原点 $O$ 出发，以每秒1个单位长度的速度沿 $x$ 轴正方向运动．过点 $P$ 作 $x$ 轴的垂线，分别交直线 $A C$ ， $A B$ 于点 $D$ ， $E$ ．设点 $P$ 运动的时间为 $t$ ．点 $D$ 的坐标为，点 $E$ 的坐标为；（均用含 $t$ 的式子表示）

(3)、在（2）的条件下，当点 $P$ 在线段 $O A$ 上时，探究是否存在某一时刻，使 $D E = O B$ ？若存在，求出此时 $△ A D E$ 的面积；若不存在，请说明理由．

(4)、在（2）的条件下，点 $Q$ 是线段 $O A$ 上一点，当点 $P$ 在射线 $O A$ 上时，探究是否存在某一时刻，使 $D E = \frac{1}{2} O P$ ？若存在，求出此时 $t$ 的值，并直接写出此时 $△ D E Q$ 为等腰三角形时点 $Q$ 的坐标；若不存在，请说明理由．

查看试题解析

备用体育用品	篮球	排球	羽毛球拍
单位（元）	50	40	25

【提升版】北师大版数学八年级上册第五章 二元一次方程组 章节测试卷

一、选择题（每题3分，共24分）

二、填空题（每题3分，共15分）

三、解答题（共7题，共61分）

【提升版】北师大版数学八年级上册第五章二元一次方程组章节测试卷