【基础版】北师大版数学八年级上册第五章二元一次方程组章节测试卷

试卷日期：2024-12-01 考试类型：单元试卷

前去【出卷网】下载

一、选择题（每题3分，共24分）

1. 下列方程中，为二元一次方程的是（）

A、 $2 a + 1 = 0$ B、 $3 x + y = z$ C、 $x = 3 y$ D、 $x y = 9$

查看试题解析
2. 二元一次方程组 $\{\begin{array}{l} x + y = 5 \\ 2 x - y = 4 \end{array}$ 的解是（　　）

A、 $\{\begin{array}{l} x = 2 \\ y = 3 \end{array}$ B、 $\{\begin{array}{l} x = 1 \\ y = 4 \end{array}$ C、 $\{\begin{array}{l} x = 4 \\ y = 1 \end{array}$ D、 $\{\begin{array}{l} x = 3 \\ y = 2 \end{array}$

查看试题解析
3. 以下是二元一次方程2x+3y＝8的正整数解有（　　）

A、 ${\begin{array}{l} x = 4 \\ y = 0 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = \frac{4}{3} \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$

查看试题解析
4. 若x＝4， $y = \frac{1}{2}$ 是方程x﹣2y＝m的解，则m的值是（）

A、﹣3 B、﹣2 C、2 D、3

查看试题解析
5. 方程2x-3y=7，用含x的代数式表示y为( )

A、 $y = \frac{7 - 2 x}{3}$ B、 $y = \frac{2 x - 7}{3}$ C、 $x = \frac{7 + 3 y}{2}$ D、 $x = \frac{7 - 3 y}{2}$

查看试题解析
6. 解方程组 ${\begin{cases} x = 3 y - 2 ① \\ 2 y - 5 x = 10 ② \end{cases}$ 时，把①代入②，得（）

A、2（3y-2）-5x=10 B、2y-（3y-2）=10 C、（3y-2）-5x=10 D、2y-5（3y-2）=10

查看试题解析
7. 若方程组 $\{\begin{array}{l} 3 x - y = 4 k - 5 \\ 2 x + 6 y = k \end{array}$ 的解中 $x + y = 2024$ ，则 $k$ 等于（）

A、2024 B、2025 C、2026 D、2027

查看试题解析
8. 2023年11月28日世界最长最宽钢壳沉管隧道——深中通道海底隧道全幅贯通，采用“西桥东隧”的方案．桥梁部分和沉管隧道总长为24千米，其中桥梁部分比沉管隧道的2倍多 $3.6$ 千米．若设桥梁部分为x千米，沉管隧道为y千米，可列方程组为（）

A、 ${\begin{array}{l} x + y = 24 \\ x = 2 y + 3.6 \end{array}$ B、 ${\begin{array}{l} x + y = 24 \\ y = 2 x + 3.6 \end{array}$ C、 ${\begin{array}{l} x + y = 24 \\ x = 2 y - 3.6 \end{array}$ D、 ${\begin{array}{l} x + y = 24 \\ y = 2 x - 3.6 \end{array}$

查看试题解析

二、填空题（每题3分，共15分）

9. 已知 ${\begin{cases} x = 2 \\ y = - 1 \end{cases}$ 是方程ax+5y=15的一个解，则a= ．

查看试题解析
10. 小强解方程组 $\{\begin{array}{l} 2 x - y = ● \\ 3 x + y = 8 \end{array}$ 时，求得方程组的解为 $\{\begin{array}{l} x = ◆ \\ y = - 1 \end{array}$ ，由于不慎，将一些墨水滴到了作业本上，刚好遮住了●处和◆处的数，那么◆处表示的数应该是

查看试题解析
11. 已知 $2 x^{n - 3} - \frac{1}{3} y^{2 m + 1} = 0$ 是关于x，y的二元一次方程，则mn= ．

查看试题解析
12. 解方程组 ${\begin{array}{l} 5 (x + y) - 3 (x - y) = 2 \\ 2 (x + y) + 4 (x - y) = 6 \end{array}$ ，若设 $(x + y) = A$ ， $(x - y) = B$ ，则原方程组可变形为．

查看试题解析
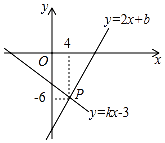
13. 如图，已知一次函数y=2x+b和y=kx﹣3（k≠0）的图象交于点P，则二元一次方程组 ${\begin{matrix} 2 x - y = - b \\ k x - y = 3 \end{matrix}$ 的解是．

查看试题解析

三、解答题（共7题，共61分）

14. 解方程组：

(1)、 $\{\begin{array}{l} 3 x + y = 15 \\ 5 x - 2 y = 14 \end{array}$ ；

(2)、 $\{\begin{array}{l} 3 x - 2 y = 7 \\ \frac{x - 2 y}{3} - \frac{2 y - 1}{2} = 1 \end{array}$ ．

查看试题解析
15. 为丰富同学们的课余活动，某校成立了篮球课外兴趣小组，计划购买一批篮球，需购买 $A$ 、 $B$ 两种不同型号的篮球共300个．已知购买3个 $A$ 型篮球和2个 $B$ 型篮球共需340元，购买2个 $A$ 型篮球和1个 $B$ 型篮球共需要210元．

(1)、求购买一个 $A$ 型篮球、一个 $B$ 型篮球各需多少元？

(2)、若该校计划投入资金 $W$ 元用于购买这两种篮球，设购进的 $A$ 型篮球为 $t$ 个，求 $W$ 关于 $t$ 的函数关系式；

(3)、学校在体育用品专卖店购买 $A$ 、 $B$ 两种型号篮球共300个，经协商，专卖店给出如下优惠： $A$ 种球每个降价8元， $B$ 种球打9折，计算下来，学校共付费16740元，学校购买 $A$ 、 $B$ 两种篮球各多少个？

查看试题解析
16. 已知 $a$ ， $b$ ， $c$ 是 $△ A B C$ 的三边．若a和b满足方程组 $\{\begin{array}{l} a + 2 b = 12 \\ 2 a - b = - 1 \end{array}$ ，且c为偶数，求这个三角形的周长．

查看试题解析
17. 某超市举行店庆活动，对甲、乙两种商品实行打折销售，打折前，购买2件甲商品和3件乙商品需要180元；购买1件甲商品和4件乙商品需要200元，而店庆期间，购买10件甲商品和10件乙商品仅需520元，这比打折前少花多少钱？

查看试题解析
18. 某校为体育节的球类比赛筹备器材。他们从体育用品商店了解到，买2个篮球和4个足球需440元；买1个篮球和3个足球需285元。

(1)、求篮球和足球的单价各是多少；

(2)、该商店在周年庆期间有“每满300减30”的优惠活动，在此期间在该店一次性购买8个篮球和10个足球共需多少元？

查看试题解析
19. 为了节能减排，我市某校准备购买某种品牌的节能灯，已知3只A型节能灯和5只B型节能灯共需50元，1只A型节能灯和3只B型节能灯共需26元．

(1)、求1只A型节能灯和1只B型节能灯的售价各是多少元．

(2)、学校准备购买这两种型号的节能灯共200只，要求购买A型号的节能灯a只，记购买两种型号的节能灯的总费用为W元．
①求W与a的函数关系式；
②当 $a = 80$ 时，求购买两种型号的节能灯的总费用是多少？

查看试题解析
20. 某公司购买了一批物资并安排两种货车运抵某市．调查得知，2辆小货车与3辆大货车一次可以满载运输1800件；3辆小货车与4辆大货车一次可以满载运输2500件．

(1)、求1辆小货车和1辆大货车一次可以分别满载运输多少件物资？

(2)、现有3200件物资需要再次运往该市，准备同时租用这两种货车，每辆均全部装满货物，有几种租车方案？请写出所有租车方案．

查看试题解析

【基础版】北师大版数学八年级上册 第五章 二元一次方程组 章节测试卷

一、选择题（每题3分，共24分）

二、填空题（每题3分，共15分）

三、解答题（共7题，共61分）

【基础版】北师大版数学八年级上册第五章二元一次方程组章节测试卷