【培优版】北师大版数学八年级上册5.8三元一次方程组同步练习

试卷日期：2024-12-01 考试类型：同步测试

前去【出卷网】下载

一、选择题

1. 三元一次方程组 $\{\begin{matrix} 3 x + 4 z = 7 \\ 2 x + 3 y + z = 9 \\ 5 x - 9 y + 7 z = 8 \end{matrix}$ 的解为（　　）

A、 $\{\begin{matrix} x = 5 \\ y = 3 \\ z = - 2 \end{matrix}$ B、 $\{\begin{matrix} x = 5 \\ y = \frac{1}{3} \\ z = 2 \end{matrix}$ C、 $\{\begin{matrix} x = 5 \\ y = \frac{1}{3} \\ z = - 2 \end{matrix}$ D、 $\{\begin{matrix} x = 5 \\ y = - \frac{1}{3} \\ z = - 2 \end{matrix}$

查看试题解析
2. 有一个牧场，牛在吃草，而草又在生长，已知饲养100头牛，草够吃25天，改为饲养84头牛，草可多吃10天，那么饲养94头牛，经过（　　）天，草便吃完．

A、33 B、32 C、30 D、28

查看试题解析
3. 购买铅笔7支，作业本3本，圆珠笔1支共需3元；购买铅笔10支，作业本4本，圆珠笔1支共需4元，则购买铅笔11支，作业本5本，圆珠笔2支共需（　）

A、4.5元 B、5元 C、6元 D、6.5元

查看试题解析
4. 矩形ABCD内放入两张边长分别为a和b（a＞b）的正方形纸片，按照图①放置，矩形纸片没有被两个正方形覆盖的部分（黑色阴影部分）的面积为S₁；按照图②放置，矩形纸片没有被两个正方形覆盖的部分面积为S₂；按图③放置，矩形纸片没有被两个正方形覆盖的部分的面积为S₃ ，已知S₁﹣S₃＝3，S₂﹣S₃＝12，设AD﹣AB＝m ，则下列值是常数的是（）

A、ma B、mb C、m D、a+b

查看试题解析
5. 七年级三个班组织部分同学参加数学和英语竞赛，且每人只允许参加其中一种，参加英语竞赛的人数是参加数学竞赛人数的 $\frac{5}{6}$ ，且比参加数学竞赛的少10人．已知，一班参赛人数占总参赛人数的 $\frac{2}{5}$ ，二班和三班参赛人数之比为5：6，则三个班的参赛人数分别是（　　）

A、22，15，18 B、33，25，30 C、44，30，36 D、55，25，30

查看试题解析
6. 小明和小亮在一起探究一个数学活动.首先小亮站立在箱子上，小明站立在地面上（如图1），然后交换位置（如图2），测量的数据如图所示，想要探究的问题有：①小明的身高；②小亮的身高；③箱子的高度；④小明与小亮的身高和.根据图上信息，你认为可以计算出的是（）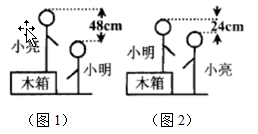

A、① B、② C、③ D、④

查看试题解析
7. 《九章算术》是我国古代著名的数学专著，其“方程”章中给出了“遍乘直除”的算法解方程组．比如对于方程组， ${\begin{array}{l} 3 x + 2 y + z = 39 ① \\ 2 x + 3 y + z = 34 ② \\ x + 2 y + 3 z = 26 ③ \end{array}$ ，先将方程①中的未知数系数排成数列 $32139$ ，然后执行如下步骤：（如图）第一步，将方程②中的未知数系数乘以3，然后不断地减一行，直到第二行第一个数变为0；第二步，对第三行做同样的操作，其余步骤都类似．
方程①： $32139$
第一步方程②： $23134 \to 693102 ⋯ ⋯ \to 051 a$
第二步方程③： $12326 \to M ⋯ ⋯ \to 0 b 839$
其实以上步骤的本质就是在消元，根据以上操作，有下列结论：（1）数列M为： $369618$ （2） $a ＝ 24$ （3） $b ＝ 4$ 其中正确的有（）

A、（1）（2） B、（2）（3） C、（1）（3） D、（1）（2）（3）

查看试题解析
8.
如图1，天平呈平衡状态，其中左侧秤盘中有一袋玻璃球，右侧秤盘中也有一袋玻璃球，还有2个各10克的砝码，将左侧袋中一颗玻璃球移至右侧秤盘，并拿走右侧秤盘的1个砝码后，天平仍呈平衡状态，如图2，现从图2右侧盘中拿掉砝码和袋子外面的玻璃球，只剩下一小袋玻璃球，要使天平保持平衡，则左侧袋中需拿出玻璃球的个数为（　　）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

9. 火锅是重庆的一张名片，深受广大市民的喜爱.重庆某火锅店采取堂食、外卖、店外摆摊（简称摆摊）三种方式经营，6月份该火锅店堂食、外卖、摆摊三种方式的营业额之比为3：5：2.随着促进消费政策的出台，该火锅店老板预计7月份总营业额会增加，其中摆摊增加的营业额占总增加的营业额的，则摆摊的营业额将达到7月份总营业额的，为使堂食、外卖7月份的营业额之比为8：5，则7月份外卖还需增加的营业额与7月份总营业额之比是.

查看试题解析
10. 为确保信息安全，信息需要加密传输，发送方由明文→密文（加密），接收方由密文→明文（解密），已知约定的加密规律为：明文x、y、z分别对应加密文x+2y、2x+3y、4z．例如：明文1、2、3分别对应加密文5、8、12，如果接收到密文为7、12、16时，则解密得到的明文是：．

查看试题解析
11. 小梦在某购物平台上购买甲、乙、丙三种商品，当购物车内选择 3 件甲、 2 件乙、 1 件丙时显示的价格为 420 元；当购物车内选择 2 件甲、 3 件乙、 4 件丙时显示的价格为 580 元，那么购买甲、乙、丙各两件应该付款

查看试题解析
12. 某商店中销售水果时采用了三种组合搭配的方式进行销售，甲种搭配是：2千克A水果，4千克B水果；乙种搭配是：3千克A水果，8千克B水果，1千克C水果；丙种搭配是：2千克A水果，6千克B水果，1千克C水果；如果A水果每千克售价为2元，B水果每千克售价为1.2元，C水果每千克售价为10元，某天，商店采用三种组合搭配的方式进行销售后共得销售额441.2元，并且A水果销售额116元，那么C水果的销售额是元．

查看试题解析
13. 11 月某花店从花农处进货了甲、乙、丙三种鲜花，数量分别为 $a ， b ， c$ ，甲、乙、丙三种鲜花单价之比为 $1 ： 3 ： 5$ ，由于近期销售火爆， 12 月花农对这三种鲜花的价格进行了调整，该花店也相应调整了进货量，相较于 11 月，花店采购甲增加的费用占 12 月所有鲜花采购费用的 $\frac{1}{5} ， 12$ 月采购甲与乙的总费用之比为 $2 ： 3$ ， 11 月采购乙的总费用与 12 月采购乙的总费用之比为 $1 ： 2$ ，采购甲、乙、丙三种鲜花增加的费用之比为 $6 ： 7 ： 5$ ，则 $a ： b ： c$ 为

查看试题解析

三、解答题

14. 解下列方程组．

(1)、 $\{\begin{matrix} x + y + z = 4, \\ 2 x - y + z = 3, \\ - x + 2 y - z = - 1 . \end{matrix}$

(2)、 $\{\begin{matrix} a + b + c = 6, \\ a - b - c = - 4, \\ 2 a + 3 b + c = 11 . \end{matrix}$

(3)、 $\{\begin{matrix} x - 4 y + z = - 3, \\ 2 x + y - z = 18, \\ x - y - z = 7 . \end{matrix}$

(4)、 $\{\begin{matrix} 2 x + 3 y + 4 z = 15, \\ 4 x + 6 y - 3 z = 8, \\ x - 2 y + z = - 5 . \end{matrix}$

查看试题解析
15. 在解决“已知有理数x、y、z满足方程组 ${\begin{array}{l} 2 x + 3 y - z = 5 ① \\ x - 2 y + 3 z = 1 ② \end{array}$ ，求 $4 x + 13 y - 9 z$ 的值”时，小华是这样分析与解答的．
解：由① $\times a$ 得： $2 a x + 3 a y - a z = 5 a$ ③，由② $\times b$ 得： $b x - 2 b y + 3 b z = b$ ④．
③＋④得： $(2 a + b) x + (3 a - 2 b) y + (- a + 3 b) z = 5 a + b$ ⑤．
当 $(2 a + b) x + (3 a - 2 b) y + (- a + 3 b) z = 4 x + 13 y - 9 z$ 时，
即 ${\begin{array}{l} 2 a + b = 4 \\ 3 a - 2 b = 13 \\ - a + 3 b = - 9 \end{array}$ ，解得 ${\begin{array}{l} a = 3 \\ b = - 2 \end{array}$ ．
∴① $\times 3 +$ ② $\times (- 2)$ ，得 $4 x + 13 y - 9 z = 5 \times 3 + 1 \times (- 2) = 13$ ．
请你根据小华的分析过程，解决如下问题：

(1)、若有理数a、b满足 $(3 x + 4 y + 2 z) \times a + (x + 6 y + 5 z) \times b = 12 x + 2 y - 5 z$ ，求a、b的值；

(2)、母亲节将至，小新准备给妈妈购买一束组合鲜花，若购买2枝红花、3枝黄花、1枝粉花共需18元；购买3枝红花、5枝黄花、2枝粉花共需28元．则购买1枝红花、3枝黄花、2枝粉花共需多少元？

查看试题解析
16. 数学活动：探究不定方程
小北，小仑两位同学在学习方程过程中，发现三元一次方程组 ${\begin{array}{l} 3 x + 2 y + z = 9 \\ 2 x + 3 y + 4 z = 11 \end{array} \begin{array}{l} ① \\ ② \end{array}$ ，虽然解不出x，y，z的具体数值，但可以解出 $x + y + z$ 的值．

(1)、小北的方法： $② \times 3 - ① \times 2$ ，整理可得： $y =$ ；
$① \times 3 - ② \times 2$ ，整理可得： $x =$ ， ∴ $x + y + z = 4$ ．
小仑的方法： $① + ②$ ：③；∴得： $x + y + z = 4$ ．

(2)、已知 ${\begin{array}{l} 3 x + y + 2 z = 9 \\ x - 3 y - z = 3 \end{array}$ ，试求解 $x + y + z$ 的值．

(3)、学校现准备采购若干英语簿，数学簿以及作文本，已知采购4本英语簿，5本数学簿，2本作文本需要6元；采购4本英语簿，8本数学簿，2本作文本需要7.2元，那么采购200本英语簿，300本数学簿，100本作文本需要多少钱？

查看试题解析

【培优版】北师大版数学八年级上册5.8三元一次方程组 同步练习

一、选择题

二、填空题

三、解答题

【培优版】北师大版数学八年级上册5.8三元一次方程组同步练习